
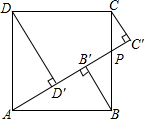
 如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为________,最小值为________.
如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与B点或C点重合),分别过B、C、D作射线AP的垂线,垂足分别是B′、C′、D′,则BB′+CC′+DD′的最大值为________,最小值为________.
 AP×CC′,根据S正方形ABCD=S△ABP+S△ADP+S△DPC,推出BB′+DD′+CC′=
AP×CC′,根据S正方形ABCD=S△ABP+S△ADP+S△DPC,推出BB′+DD′+CC′=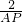 ,根据已知得出1≤AP≤
,根据已知得出1≤AP≤ ,
,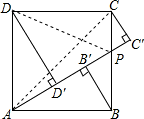
 =
= ,
, ,
, AP×CC′,
AP×CC′, AP(BB′+DD′+CC′),
AP(BB′+DD′+CC′),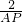 ,
, ,
, ≤BB′+CC′+DD′≤2,
≤BB′+CC′+DD′≤2, .
.

科目:初中数学 来源: 题型:
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com