
 在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=
在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF= ∠DAB,试猜想当∠B与∠D满足________时,可使得DE+BF=EF.
∠DAB,试猜想当∠B与∠D满足________时,可使得DE+BF=EF. ∠DAB,所以得到∠EAF=∠GAF,再利用SAS证明△AEF≌△AGF,然后根据全等三角形的性质就可以证明DE+BF=EF.
∠DAB,所以得到∠EAF=∠GAF,再利用SAS证明△AEF≌△AGF,然后根据全等三角形的性质就可以证明DE+BF=EF.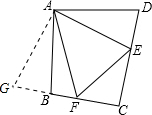 解:当∠ABC+∠D=180°时,DE+BF=EF.理由如下:
解:当∠ABC+∠D=180°时,DE+BF=EF.理由如下: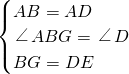 ,
, ∠DAB=
∠DAB= ∠DAB,
∠DAB,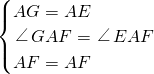 ,
,

 优生乐园系列答案
优生乐园系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com