
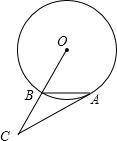
 如图,已知弦AB与半径相等,连接OB,并延长使BC=OB.
如图,已知弦AB与半径相等,连接OB,并延长使BC=OB.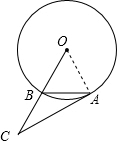 解:(1)AC是⊙O的切线.
解:(1)AC是⊙O的切线.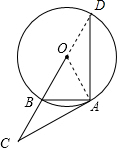
 ∠AOB=30°,
∠AOB=30°,

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
 |
| AC |
 |
| CE |
| 1 |
| 2 |
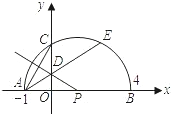 两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.查看答案和解析>>
科目:初中数学 来源:新教材新学案数学九年级上册 题型:013
如图,C是以AB为直径的半圆弧上的一点,已知BC的弦心距与直径AB的比为![]() ∶4,则
∶4,则![]() 所对的圆心角为
所对的圆心角为

A.100°
B.90°
C.115°
D.120°
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(36):2.7 最大面积是多少(解析版) 题型:解答题
 与
与 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(39):2.3 二次函数的应用(解析版) 题型:解答题
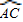 与
与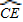 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.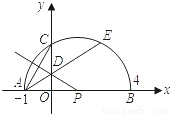
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》中考题集(39):27.3 实践与探索(解析版) 题型:解答题
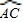 与
与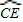 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.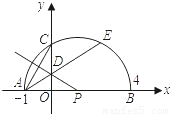
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com