
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
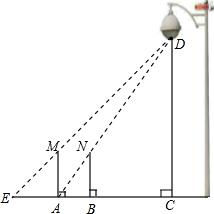 (2013•陕西)一天晚上,黎明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).
(2013•陕西)一天晚上,黎明和张龙利用灯光下的影子长来测量一路灯D的高度.如图,当李明走到点A处时,张龙测得李明直立时身高AM与影子长AE正好相等;接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25m,已知李明直立时的身高为1.75m,求路灯的高CD的长.(结果精确到0.1m).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com