
【题目】如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD. 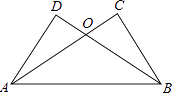
求证:
(1)BC=AD;
(2)△OAB是等腰三角形.
【答案】
(1)证明:∵AC⊥BC,BD⊥AD,
∴∠ADB=∠ACB=90°,
在Rt△ABC和Rt△BAD中,
∵ ![]() ,
,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD
(2)证明:∵Rt△ABC≌Rt△BAD,
∴∠CAB=∠DBA,
∴OA=OB,
∴△OAB是等腰三角形
【解析】(1)根据AC⊥BC,BD⊥AD,得出△ABC与△BAD是直角三角形,再根据AC=BD,AB=BA,得出Rt△ABC≌Rt△BAD,即可证出BC=AD,(2)根据Rt△ABC≌Rt△BAD,得出∠CAB=∠DBA,从而证出OA=OB,△OAB是等腰三角形.
【考点精析】本题主要考查了等腰三角形的判定的相关知识点,需要掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等才能正确解答此题.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】已知AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于 ![]() EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为度.
EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=116°,则∠DHB的大小为度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材中,在计算如图1所示的正方形ABCD的面积时,分别从两个不同的角度进行了操作:
(1)把它看成是一个大正方形,则它的面积为 ![]() ;
;
(2)把它看成是2个小长方形和2个小正方形组成的,则它的面积为 ![]() ;因此,可得到等式:
;因此,可得到等式: ![]() .
.
① 类比教材中的方法,由图2中的大正方形可得等式:
.
② 试在图2右边空白处画出面积为 ![]() 的长方形的示意图(标注好a、b),由图形可知,多项式
的长方形的示意图(标注好a、b),由图形可知,多项式 ![]() 可分解因式为:
可分解因式为:
. 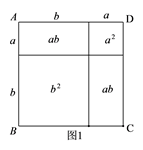
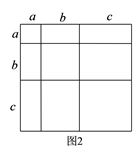
在上方空白处画出②中的示意图
③ 若将代数式 ![]() 展开后合并同类项,得到多项式N,则多项式N的项数一共有项.
展开后合并同类项,得到多项式N,则多项式N的项数一共有项.
查看答案和解析>>
科目:初中数学 来源: 题型:
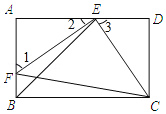
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.
(1)求证:△AEF≌△DCE;
(2)若CD=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例. 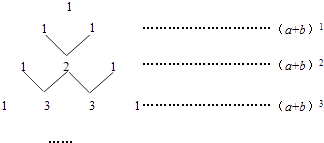
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当a < 0 时,方程ax2+bx+c=0无实数根,则二次函数y=ax2+bx+c的图像一定在 ( )
A、x轴上方 B、x轴下方 C、y轴右侧 D、y轴左侧
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com