
 作出函数y=$\frac{2}{x+1}$的图象,并求当$\frac{1}{2}$≤x≤3时,函数的最大值和最小值.
作出函数y=$\frac{2}{x+1}$的图象,并求当$\frac{1}{2}$≤x≤3时,函数的最大值和最小值. 分析 由函数图象可知当x>-1时,y随x的增大而减小,则可求得当$\frac{1}{2}$≤x≤3时函数的最大值和最小值.
解答 解:
函数图象如图所示,
由图象可知当当x>-1时,y随x的增大而增大,
∴当$\frac{1}{2}$≤x≤3时,当x=$\frac{1}{2}$时函数有最大值,最大值为y=$\frac{2}{\frac{1}{2}+1}$=$\frac{4}{3}$,
当x=3时函数有最小值,最小值为y=$\frac{2}{3+1}$=$\frac{1}{2}$,
∴当$\frac{1}{2}$≤x≤3时,函数的最大值是$\frac{4}{3}$,最小值是$\frac{1}{2}$.
点评 本题主要考查反比例函数的性质,掌握反比例函数的增减性是解题的关键,注意数形结合.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(2,0),P是函数y=x(x>0)图象上一点,PQ⊥AP交y轴于点Q.设点P的横坐标为a,点Q的纵坐标为b,若OP<10$\sqrt{2}$,求b的取值范围.
如图,在平面直角坐标系中,已知点A(2,0),P是函数y=x(x>0)图象上一点,PQ⊥AP交y轴于点Q.设点P的横坐标为a,点Q的纵坐标为b,若OP<10$\sqrt{2}$,求b的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
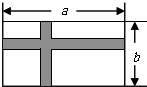 如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化.
如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com