
分析 (1)分别根据0指数幂及负整数指数幂的计算法则、数的开方法则、特殊角的三角函数值分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把m=-3代入进行计算即可.
解答 解:(1)原式=3+1-5-$\sqrt{2}$
=-$\sqrt{2}$-1;
(2)原式=[$\frac{(m+1)(m-1)}{(m-1)^{2}}$+$\frac{m}{m(m-1)}$]÷$\frac{m+2}{m}$
=($\frac{m+1}{m-1}$+$\frac{1}{m-1}$)÷$\frac{m+2}{m}$
=$\frac{m+2}{m-1}$•$\frac{m}{m+2}$
=$\frac{m}{m-1}$,
当m=-3时,原式=$\frac{-3}{-3-1}$=$\frac{3}{4}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
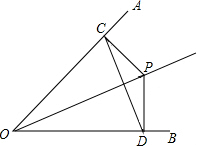 如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{30}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{27a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
| 优等品频率$\frac{m}{n}$ | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com