
【题目】在等边△ABC的外侧作直线BM,点A关于直线BM的对称点为D,连结AD,CD,设CD交直线BM于点E.
(1)依题意补全图1,若∠ABM=30°,求∠BCE的度数;
(2)如图2,若60°<∠ABM<90°,判断直线BM和CD相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由.
【答案】
(1)解:补全的图1如下所示:
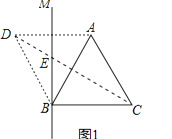
连接BD,如上图1所示,
∵由已知可得,BM垂直平分AD,∠ABM=30°,△ABC是等边三角形,
∴△BDA是等边三角形,AD∥BC且AD=BC,DA=DB,
∴四边形ADBC是菱形,
∵∠ACB=60°,
∴∠BCE=30°;
(2)解:直线BM和CD相交所成的锐角的度数是定值,如下图所示,
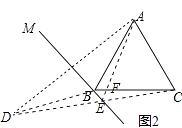
连接AE交BC于点F,
由已知可得,BD=BA,BA=BC,ED=EA,
则∠BDA=∠BAD,∠EDA=∠EAD,BD=BC,
∴∠BDC=∠BCD,∠EDB=∠EAB,
∴∠BCD=∠EAB,
∵∠EFC=∠BFA,∠ABC=60°,
∴∠CEA=∠ABC=60°,
∵∠AEC+∠AEM+∠DEM=180°,∠DEM=∠AEM,
∴∠DEM=60°,
即直线BM和CD相交所成的锐角的度数是定值,这个锐角的度数是60°.
【解析】(1)连接BD,由作图知:BM垂直平分AD根据中垂线定理及等腰三角形的三线合一得出△BDA是等边三角形,由△ABC是等边三角形,故AD∥BC且AD=BC,DA=DB,从而判断出四边形ADBC是菱形,根据菱形的每条对角线平分一组对角得出答案;
(2)直线BM和CD相交所成的锐角的度数是定值,连接AE交BC于点F,根据等边对等角及等量代换得出∠BDA=∠BAD,∠EDA=∠EAD,BD=BC,从而得出∠BDC=∠BCD,∠EDB=∠EAB,根据等量代换得出∠BCD=∠EAB,又由∠AEC+∠AEM+∠DEM=180°,∠DEM=∠AEM,∠CEA=∠ABC=60°,从而得出∠DEM=60°,即直线BM和CD相交所成的锐角的度数是定值,这个锐角的度数是60°.
【考点精析】关于本题考查的角的运算和线段垂直平分线的性质,需要了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】在数轴上,点 A,B 在原点 O 的两侧,分别表示数 a,2,将点 A 向右移动 1 个单位长度,得到点 C, 若 CO=BO,则 a 的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜薹共用去16万元.
(1)求两批次购进蒜薹各多少吨;
(2)公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在彩虹读书活动中,某校决定为八年级学生购买同等数量的《钢铁是怎样炼成的》和《居里夫人自传》,供学生借阅.其中《居里夫人自传》的单价比《钢铁是怎样炼成的》的单价多8元.若学校购买《居里夫人自传》用了1 000元,购买《钢铁是怎样炼成的》用了600元,请问两种书的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB= , AC= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且平分的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个边长不定的正方形![]() ,它的两个相对的顶点
,它的两个相对的顶点![]() 分别在边长为1的正六边形一组平行的对边上,另外两个顶点
分别在边长为1的正六边形一组平行的对边上,另外两个顶点![]() 在正六边形内部(包括边界),则正方形边长
在正六边形内部(包括边界),则正方形边长![]() 的取值范围是 .
的取值范围是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC,AD,AB于点E,O,F,连接OC,OB,则图中全等的三角形有( )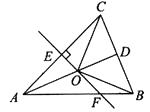
A.1对
B.2对
C.3对
D.4对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com