
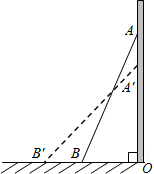
 如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米?
如图,一架10米长的梯子斜靠在墙上,刚好梯顶抵达8米高的路灯.当电工师傅沿梯上去修路灯时,梯子下滑到了B′处,下滑后,两次梯脚间的距离为2米,则梯顶离路灯多少米?  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
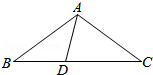 如图,在△ABC中,D是BC上一点,若∠B=∠C=∠BAD,∠DAC=∠ADC,∠BAC的度数为( )
如图,在△ABC中,D是BC上一点,若∠B=∠C=∠BAD,∠DAC=∠ADC,∠BAC的度数为( )| A. | 36度 | B. | 72度 | C. | 98度 | D. | 108度 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com