平面上任意五个点都落在格点上,试证明至少有二个点连线的中点也在格点上.
【答案】
分析:首先根据中点坐标公式知,坐标平面两点(x
1,y
1)、(x
2,y
2)的中点坐标是(
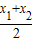
,
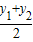
),再证明x
1与x
2,y
1与y
2的奇偶性相同,根据坐标的奇偶性构造四个“抽屉”进行证明.
解答:证明:由中点坐标公式知,坐标平面两点(x
1,y
1)、(x
2,y
2)的中点坐标是(
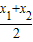
,
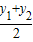
).
欲使

和
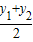
都是整数,必须而且只须x
1与x
2,y
1与y
2的奇偶性相同.
平面上格点的坐标是以下四种情况:(奇数,奇数),(奇数,偶数),(偶数,偶数),
(偶数,奇数)由于五个点都落在格点上,肯定有二个格点的坐标情况相同,
根据整数的奇偶性质,则他们连线的中点坐标也一定是以上四种情况之一.
故至少有二个点的中点的连线也在格点上.
点评:此题主要考查了抽屉原理的知识点,解答本题的关键是对坐标平面上的任意格点按照横纵两个坐标的奇偶性考虑构造四个“抽屉”,充分利用好抽屉原理的知识点,本题难度较大.

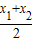 ,
,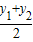 ),再证明x1与x2,y1与y2的奇偶性相同,根据坐标的奇偶性构造四个“抽屉”进行证明.
),再证明x1与x2,y1与y2的奇偶性相同,根据坐标的奇偶性构造四个“抽屉”进行证明.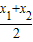 ,
,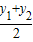 ).
). 和
和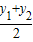 都是整数,必须而且只须x1与x2,y1与y2的奇偶性相同.
都是整数,必须而且只须x1与x2,y1与y2的奇偶性相同.
