
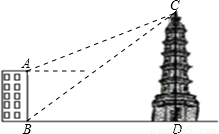
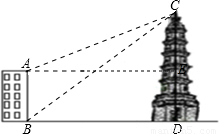
 解:过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=38.5°,ED=AB=16米
解:过点A作AE⊥CD于点E,由题意可知:∠CAE=22°,∠CBD=38.5°,ED=AB=16米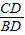
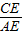


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
 38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )
38.5°≈0.62,cos38.5°≈0.78,tan38.5°≈0.80 )查看答案和解析>>
科目:初中数学 来源: 题型:
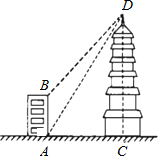 如图,大楼AB的高为16米,远处有一塔CD,小明在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°.其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求:
如图,大楼AB的高为16米,远处有一塔CD,小明在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°.其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求:查看答案和解析>>
科目:初中数学 来源:2012年辽宁省锦州市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2012年4月份中考数学模拟试卷(十五)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com