
 ,则代数式
,则代数式 -
-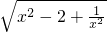 的值为________.
的值为________. 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:阅读理解
|
查看答案和解析>>
科目:初中数学 来源:百分学生作业本课时3练1测 七年级数学(下) 适用人教课标版学生 人教课标版 题型:013
用代入法解方程组![]() 可转化成解一元一次方程的问题,若消去x,则含y的一元一次方程的标准形式为
可转化成解一元一次方程的问题,若消去x,则含y的一元一次方程的标准形式为
A.y=1
B.4y=3
C.-21y=-14
D.3y=8
查看答案和解析>>
科目:初中数学 来源:三点一测丛书八年级数学上 题型:044
大家知道,解方程是否正确,可以把得出的未知数的值代入方程检验,而解不等式的解集里往往有无数个数值,不可能将这些数值一一代入原不等式进行检验.那么,解不等式所得的结果是否能正确检验呢?
解一元一次不等式的一般步骤与解一元一次方程基本一致,只是在去分母及系数化为1时,两边同乘以(或除以)同一个负数,不等号方向要改变方向,因此,解不等式正确与否,可以仿照解方程的代入检验.
①若求得的一元一次不等式的解集为x>a(或x<a),则令x=a,把x=a代入不等式的左右两边,若两边相等,则求得的不等式的解集可能是正确的,若两边不相等,则一定错了.
②取符合x>a(或x<a)的一个特殊数b,分别代入原不等式的左右两边,若适合原不等式,则求得的不等式解集一定正确,若不适合原不等式,则只要改变x>a(或x<a=的不等号方向即可.
请你用上面介绍的方法检验一下x>5是不是不等式1+![]() >5-
>5-![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源:初中数学 三点一测丛书 八年级数学 下 (江苏版课标本) 江苏版 题型:044
大家知道,解方程是否正确,可以把得出的未知数的值代入方程检验,而解
等式的解集里往往有无数个数值,不可能将这些数值一一代入原不等式进行检验.那么,解不等式所得的结果是否能正确检验呢?
解一元一次不等式的一般步骤与解一元一次方程基本一致,只是在去分母及系数化为1时,两边同乘以(或除以)同一个负数,不等号要改变方向,因此,解不等式正确与否,可以仿照解方程的代入检验.
(1)若求得的一元一次不等式的解集为x>a(或x<a),则令x=a,把x=a代入不等式的左右两边,若两边相等,则求得的不等式的解集可能是正确的,若两边不相等,则一定错了.
(2)取符合x>a(或x<a)的一个特殊数b,分别代入原不等式的左右两边,若适合原不等式,则求得的不等式解集一定正确,若不适合原不等式,则只要改变x>a(或x<a)的不等号方向即可.
请你用上面介绍的方法检验一下x>5是不是不等式1+![]() >5-
>5-![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源:2008年江苏省南京市高淳县中考数学二模试卷(解析版) 题型:解答题
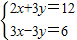 的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组
的求解方法是消元法,即可将它化为一元一次方程来解,可求得方程组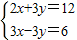 有唯一解.
有唯一解.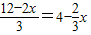
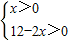 则有0<x<6
则有0<x<6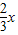 为正整数,则
为正整数,则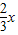 为正整数,所以x为3的倍数
为正整数,所以x为3的倍数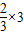 =2
=2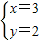
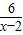 为正整数,则满足条件的x的值有几个.( )
为正整数,则满足条件的x的值有几个.( )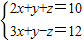 的正整数解.
的正整数解.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com