
 在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍
在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍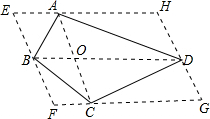 解:(1)能实现,l分
解:(1)能实现,l分

科目:初中数学 来源: 题型:
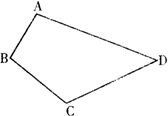 32、如图,某村有一个四边形的池塘,在它的四个角A、B、C、D处各有一棵古树,现村民要在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍
32、如图,某村有一个四边形的池塘,在它的四个角A、B、C、D处各有一棵古树,现村民要在不移动古树,并且池塘各边保持直线的情况下,把池塘的面积增大一倍查看答案和解析>>
科目:初中数学 来源: 题型:
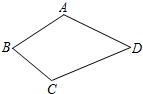 18、如图,某村有一个四边形的池塘,在它的四个顶点A、B、C、D处均有一棵树,该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持树不动,并要求扩建后的池塘成平行四边形形状,请问该村能否实现这一设想?
18、如图,某村有一个四边形的池塘,在它的四个顶点A、B、C、D处均有一棵树,该村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持树不动,并要求扩建后的池塘成平行四边形形状,请问该村能否实现这一设想?查看答案和解析>>
科目:初中数学 来源:山东省期中题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年天津市西青区中考数学一模试卷(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com