Question

【题目】如图，AB是⊙O的直径，C是BD的中点，CE⊥AB，垂足为E，BD交CE于点F．

【1】求证：CF=BF；

【2】若AD=2，⊙O的半径为3，求BC的长

Answer 1

【答案】

【1】连结AC，如图

∵C是弧BD的中点 ∴∠BDC=∠DBC

又∠BDC=∠BAC

在三角形ABC中，∠ACB=90°，CE⊥AB∴ ∠BCE=∠BAC，

∠BCE=∠DBC

∴ CF=BF 因此，CF=BF． 3分

【2】证法一：作CG⊥AD于点G，

∵C是弧BD的中点 ∴∠CAG=∠BAC，

即AC是∠BAD的角平分线．

∴ CE=CG，AE="AG" ，在Rt△BCE与Rt△DCG中，CE="CG" ，CB=CD

∴Rt△BCE≌Rt△DCG，∴BE="DG" ，∴AE=AB-BE=AG=AD+DG即 6-BE=2+DG

∴2BE=4，即BE=2 又 △BCE∽△BAC，∴

（舍去负值），∴7分

（2）证法二：∵AB是⊙O的直径，CE⊥AB

∴∠BEF=，

在与中，

∵

∴∽，则

即， ∴

又∵， ∴

利用勾股定理得：

又∵△EBC∽△ECA则，即则

∴即

∴∴

【解析】试题分析：连接AC，根据已知条件利用等角对等边可以得到CF=BF；作CG⊥AD于点G，先利用HL判定Rt△BCE≌Rt△DCG，推出BE=DG/span>，根据边之间的关系可求得BE的值，再根据相似三角形的判定得到△BCE∽△BAC，根据相似三角形的对应边成比例，可得到BC2=BEAB，这样便求得BC的值，注意负值要舍去．

试题解析：（1）连接AC，如图

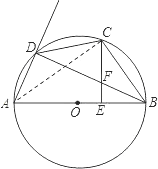
∵C是弧BD的中点

∴∠BDC=∠DBC

又∵∠BDC=∠BAC

在△ABC中，∠ACB=90°，CE⊥AB

∴∠BCE=∠BAC

∠BCE=∠DBC

∴CF=BF；

（2）作CG⊥AD于点G，

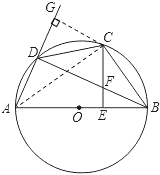
∵C是弧BD的中点

∴∠CAG=∠BAC，

即AC是∠BAD的角平分线．

∴CE=CG，AE=AG

在Rt△BCE与Rt△DCG中，

CE=CG，CB=CD

∴Rt△BCE≌Rt△DCG（HL）

∴BE=DG

∴AE=AB-BE=AG=AD+DG

即6-BE=2+DG

∴2BE=4，即BE=2

又∵△BCE∽△BAC

∴BC2=BEAB=12

BC=±2（舍去负值）

∴BC=2．