
ЁОЬтФПЁПОХФъМЖЃЈ3ЃЉАрЪ§бЇаЫШЄаЁзщОЙ§ЪаГЁЕїВщећРэГіФГжжЩЬЦЗдкЕкxЬьЃЈ1ЁмxЁм90ЃЌЧвxЮЊећЪ§ЃЉЕФЪлМлгыЯњЪлСПЕФЯрЙиаХЯЂШчЯТЃЎвбжЊЩЬЦЗЕФНјМлЮЊ30дЊ/МўЃЌЩшИУЩЬЦЗЕФЪлМлЮЊyЃЈЕЅЮЛЃКдЊ/МўЃЉЃЌУПЬьЕФЯњЪлСПЮЊpЃЈЕЅЮЛЃКМўЃЉЃЌУПЬьЕФЯњЪлРћШѓЮЊwЃЈЕЅЮЛЃКдЊЃЉЃЎ
ЪБМфxЃЈЬьЃЉ | 1 | 30 | 60 | 90 |
УПЬьЯњЪлСПpЃЈМўЃЉ | 198 | 140 | 80 | 20 |

ЃЈ1ЃЉЧѓГіwгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЮЪЯњЪлИУЩЬЦЗЕкМИЬьЪБЃЌЕБЬьЕФЯњЪлРћШѓзюДѓЃПВЂЧѓГізюДѓРћШѓЃЛ
ЃЈ3ЃЉИУЩЬЦЗдкЯњЪлЙ§ГЬжаЃЌЙВгаЖрЩйЬьУПЬьЕФЯњЪлРћШѓВЛЕЭгк5600дЊЃПЧыжБНгаДГіНсЙћЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКЕБ1ЁмxЁм50ЪБЃЌЩшЩЬЦЗЕФЪлМлyгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЮЊy=kx+bЃЈkЁЂbЮЊГЃЪ§ЧвkЁй0ЃЉЃЌ
Ёпy=kx+bОЙ§ЕуЃЈ0ЃЌ40ЃЉЁЂЃЈ50ЃЌ90ЃЉЃЌ
Ёр ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌ
ЃЌ
ЁрЪлМлyгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЮЊy=x+40ЃЛ
ЕБ50ЁмxЁм90ЪБЃЌy=90ЃЎ
ЁрЪлМлyгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЮЊy= ![]() ЃЎ
ЃЎ
гЩЪ§ОнПЩжЊУПЬьЕФЯњЪлСПpгыЪБМфxГЩвЛДЮКЏЪ§ЙиЯЕЃЌ
ЩшУПЬьЕФЯњЪлСПpгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЮЊp=mx+nЃЈmЁЂnЮЊГЃЪ§ЃЌЧвmЁй0ЃЉЃЌ
Ёпp=mx+nЙ§ЕуЃЈ60ЃЌ80ЃЉЁЂЃЈ30ЃЌ140ЃЉЃЌ
Ёр ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌ
ЃЌ
Ёрp=Љ2x+200ЃЈ0ЁмxЁм90ЃЌЧвxЮЊећЪ§ЃЉЃЌ
ЕБ1ЁмxЁм50ЪБЃЌw=ЃЈyЉ30ЃЉp=ЃЈx+40Љ30ЃЉЃЈЉ2x+200ЃЉ=Љ2x2+180x+2000ЃЛ
ЕБ50ЁмxЁм90ЪБЃЌw=ЃЈ90Љ30ЃЉЃЈЉ2x+200ЃЉ=Љ120x+12000ЃЎ
злЩЯЫљЪОЃЌУПЬьЕФЯњЪлРћШѓwгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЪЧw= ![]()
ЃЈ2ЃЉНтЃКЕБ1ЁмxЁм50ЪБЃЌw=Љ2x2+180x+2000=Љ2ЃЈxЉ45ЃЉ2+6050ЃЌ
Ёпa=Љ2ЃМ0Чв1ЁмxЁм50ЃЌ
ЁрЕБx=45ЪБЃЌwШЁзюДѓжЕЃЌзюДѓжЕЮЊ6050дЊЃЎ
ЕБ50ЁмxЁм90ЪБЃЌw=Љ120x+12000ЃЌ
Ёпk=Љ120ЃМ0ЃЌwЫцxдіДѓЖјМѕаЁЃЌ
ЁрЕБx=50ЪБЃЌwШЁзюДѓжЕЃЌзюДѓжЕЮЊ6000дЊЃЎ
Ёп6050ЃО6000ЃЌ
ЁрЕБx=45ЪБЃЌwзюДѓЃЌзюДѓжЕЮЊ6050дЊЃЎ
МДЯњЪлЕк45ЬьЪБЃЌЕБЬьЛёЕУЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ6050дЊ
ЃЈ3ЃЉНтЃКЕБ1ЁмxЁм50ЪБЃЌСюw=Љ2x2+180x+2000Ён5600ЃЌМДЉ2x2+180xЉ3600Ён0ЃЌ
НтЕУЃК30ЁмxЁм50ЃЌ
50Љ30+1=21ЃЈЬьЃЉЃЛ
ЕБ50ЁмxЁм90ЪБЃЌСюw=Љ120x+12000Ён5600ЃЌМДЉ120x+6400Ён0ЃЌ
НтЕУЃК50ЁмxЁм53 ![]() ЃЌ
ЃЌ
ЁпxЮЊећЪ§ЃЌ
Ёр50ЁмxЁм53ЃЌ
53Љ50+1=4ЃЈЬьЃЉЃЎ
злЩЯПЩжЊЃК21+4Љ1=24ЃЈЬьЃЉЃЌ
ЙЪИУЩЬЦЗдкЯњЪлЙ§ГЬжаЃЌЙВга24ЬьУПЬьЕФЯњЪлРћШѓВЛЕЭгк5600дЊ
ЁОНтЮіЁПЃЈ1ЃЉЕБ1ЁмxЁм50ЪБЃЌЩшЩЬЦЗЕФЪлМлyгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЮЊy=kx+bЃЌгЩЕуЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіДЫЪБyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌИљОнЭМаЮПЩЕУГіЕБ50ЁмxЁм90ЪБЃЌy=90ЃЎдйНсКЯИјЖЈБэИёЃЌЩшУПЬьЕФЯњЪлСПpгыЪБМфxЕФКЏЪ§ЙиЯЕЪНЮЊp=mx+nЃЌЬзШыЪ§ОнРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіpЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌИљОнЯњЪлРћШѓ=ЕЅМўРћШѓЁСЯњЪлЪ§СПМДПЩЕУГіwЙигкxЕФКЏЪ§ЙиЯЕЪНЃЛЃЈ2ЃЉИљОнwЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌЗжЖЮПМТЧЦфзюжЕЮЪЬтЃЎЕБ1ЁмxЁм50ЪБЃЌНсКЯЖўДЮКЏЪ§ЕФаджЪМДПЩЧѓГідкДЫЗЖЮЇФкwЕФзюДѓжЕЃЛЕБ50ЁмxЁм90ЪБЃЌИљОнвЛДЮКЏЪ§ЕФаджЪМДПЩЧѓГідкДЫЗЖЮЇФкwЕФзюДѓжЕЃЌСНИізюДѓжЕзїБШНЯМДПЩЕУГіНсТлЃЛЃЈ3ЃЉСюwЁн5600ЃЌПЩЕУГіЙигкxЕФвЛдЊЖўДЮВЛЕШЪНКЭвЛдЊвЛДЮВЛЕШЪНЃЌНтВЛЕШЪНМДПЩЕУГіxЕФШЁжЕЗЖЮЇЃЌгЩДЫМДПЩЕУГіНсТлЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌдкЁїABCжаЃЌЁЯA=90ЁуЃЌAB=ACЃЌЕуDЮЊBCЕФжаЕуЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌШєЕуEЁЂFЗжБ№ЮЊABЁЂACЩЯЕФЕуЃЌЧвDEЁЭDFЃЌЧѓжЄЃКBE=AFЃЛ
ЃЈ2ЃЉШєЕуEЁЂFЗжБ№ЮЊABЁЂCAбгГЄЯпЩЯЕФЕуЃЌЧвDEЁЭDFЃЌФЧУДBE=AFТ№ЃПЧыРћгУЭМЂкЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧДѓАыдВOЕФжБОЖЃЌAOЪЧаЁАыдВMЕФжБОЖЃЌЕуPЪЧДѓАыдВOЩЯвЛЕуЃЌPAгыаЁАыдВMНЛгкЕуCЃЌЙ§ЕуCзїCDЁЭOPгкЕуDЃЎ 
ЃЈ1ЃЉЧѓжЄЃКCDЪЧаЁАыдВMЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAB=8ЃЌЕуPдкДѓАыдВOЩЯдЫЖЏЃЈЕуPВЛгыAЃЌBСНЕужиКЯЃЉЃЌЩшPD=xЃЌCD2=yЃЎ ЂйЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЂкЕБy=3ЪБЃЌЧѓPЃЌMСНЕужЎМфЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCгыЁїAЁфBЁфCЁфЖМЪЧЕШбќШ§НЧаЮЃЌЧвAB=AC=5ЃЌAЁфBЁф=AЁфCЁф=3ЃЌШєЁЯB+ЁЯBЁф=90ЁуЃЌдђЁїABCгыЁїAЁфBЁфCЁфЕФУцЛ§БШЮЊ ЃЎ 
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШёНЧШ§НЧаЮABCжаЃЌжБЯпlЮЊBCЕФжаДЙЯпЃЌЩфЯпmЮЊЁЯABCЕФНЧЦНЗжЯпЃЌжБЯпlгыmЯрНЛгкЕуP.ШєЁЯBACЃН60ЁуЃЌЁЯACPЃН24ЁуЃЌдђЁЯABPЕФЖШЪ§ЪЧ( )

A. 24Ёу B. 30Ёу C. 32Ёу D. 36Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇОХФъМЖЪ§бЇаЫШЄаЁзщЯыВтСПНЈжўЮяABЕФИпЖШЃЎЫћУЧдкCДІбіЭћНЈжўЮяЖЅЖЫЃЌВтЕУбіНЧЮЊ48ЁуЃЌдйЭљНЈжўЮяЕФЗНЯђЧАНј6УзЕНДяDДІЃЌВтЕУбіНЧЮЊ64ЁуЃЌЧѓНЈжўЮяЕФИпЖШЃЎЃЈВтНЧЦїЕФИпЖШКіТдВЛМЦЃЌНсЙћОЋШЗЕН0.1УзЃЉ
ЃЈВЮПМЪ§ОнЃКsin48ЁуЁж ![]() ЃЌtan48ЁуЁж
ЃЌtan48ЁуЁж ![]() ЃЌsin64ЁуЁж
ЃЌsin64ЁуЁж ![]() ЃЌtan64ЁуЁж2ЃЉ
ЃЌtan64ЁуЁж2ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЪЧBCБпЩЯЕФИпЃЌBEЦНЗжЁЯABCНЛACБпгкEЃЌСНЯпЯрНЛгкFЕуЃЎ
ЃЈ1ЃЉШєЁЯBAC=60ЁуЃЌЁЯC=70ЁуЃЌЧѓЁЯAFBЕФДѓаЁЃЛ
ЃЈ2ЃЉШєDЪЧBCЕФжаЕуЃЌЁЯABE=30ЁуЃЌЧѓжЄЃКЁїABCЪЧЕШБпШ§НЧаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ AD ЮЊЁї ABC ЕФжаЯпЃЌ BE ЮЊЁї ABD ЕФжаЯпЃЎ

ЃЈ1ЃЉЁЯ ABE=15ЁуЃЌЁЯ BED=55ЁуЃЌЧѓЁЯ BAD ЕФЖШЪ§ЃЛ
ЃЈ2ЃЉзїЁї BED ЕФБп BD БпЩЯЕФИпЃЛ
ЃЈ3ЃЉШєЁї ABC ЕФУцЛ§ЮЊ 20ЃЌ BD=2.5ЃЌЧѓЁї BDE жа BD БпЩЯЕФИп.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋвЛеХжБНЧШ§НЧаЮABCжНЦЌбиаББпABЩЯЕФжаЯпCDМєПЊЃЌЕУЕНЁїACDЃЌдйНЋЁїACDбиDBЗНЯђЦНвЦЕНЁїAЁфCЁфDЁфЕФЮЛжУЃЌШєЦНвЦПЊЪМКѓЕуDЁфЮДЕНДяЕуBЪБЃЌAЁфCЁфНЛCDгкEЃЌDЁфCЁфНЛCBгкЕуFЃЌСЌНгEFЃЌЕБЫФБпаЮEDDЁфFЮЊСтаЮЪБЃЌЪдЬНОПЁїAЁфDEЕФаЮзДЃЌВЂХаЖЯЁїAЁфDEгыЁїEFCЁфЪЧЗёШЋЕШЃПЧыЫЕУїРэгЩЃЎ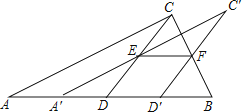
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com