
分析 由x=$\sqrt{2}$知x-2<0、6-x>0,根据分式的混合运算顺序化简原式,再代入求解可得.
解答 解:∵x=$\sqrt{2}$,
∴x-2<0、6-x>0
原式=$\frac{{x}^{2}-2x+4}{-(x-2)}$•$\frac{(x+2)(x-2)}{(x+2)({x}^{2}-2x+4)}$•$\frac{-(x-6)}{(x+1)(x-6)}$-(x2-x+1)
=$\frac{1}{x+1}$-x2+x-1
=$\frac{1}{\sqrt{2}+1}$-($\sqrt{2}$)2+$\sqrt{2}$-1
=$\sqrt{2}$-1-2+$\sqrt{2}$-1
=2$\sqrt{2}$-4.
点评 本题主要考查分式的化简求值,熟练掌握分数的混合运算顺序和法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于A,C两点(点A在点C的左边).直线y=kx+b(k≠0)分别交x轴,y轴于A,B两点,且除了点A之外,该直线与抛物线没有其它任何交点.
如图,抛物线y=-$\frac{1}{4}$x2-$\frac{1}{2}$x+$\frac{3}{4}$与x轴交于A,C两点(点A在点C的左边).直线y=kx+b(k≠0)分别交x轴,y轴于A,B两点,且除了点A之外,该直线与抛物线没有其它任何交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
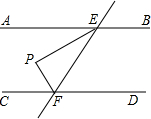 如图,AB∥CD,直线EF与AB,CD分别相交于点E、F,EP平分∠AEF,FP平分∠EFC.
如图,AB∥CD,直线EF与AB,CD分别相交于点E、F,EP平分∠AEF,FP平分∠EFC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
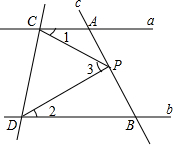 已知:如图,直线a∥b,直线c和直线a、b分别相交于A、B两点,点P在AB上.
已知:如图,直线a∥b,直线c和直线a、b分别相交于A、B两点,点P在AB上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com