
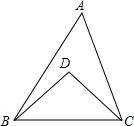
 如图所示,在△ABC中,∠A=60°,点D在△ABC的内部,并且∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,则∠D的度数是90°.
如图所示,在△ABC中,∠A=60°,点D在△ABC的内部,并且∠DBA=$\frac{1}{4}$∠ABC,∠DCA=$\frac{1}{4}$∠ACB,则∠D的度数是90°.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 月龄/月 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 体重/g | 3500 | 4200 | 4900 | 5600 | 6300 | 7000 | 7700 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
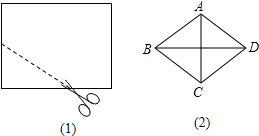 如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )| A. | 10cm2 | B. | 20cm2 | C. | 40cm2 | D. | 80cm2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com