
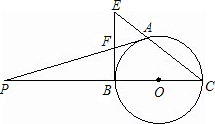
 点,F是BE的中点,延长AF,CB交于点P.
点,F是BE的中点,延长AF,CB交于点P.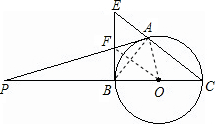 (1)证明:连接AB,OA,OF;
(1)证明:连接AB,OA,OF;

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.
(2013•南通一模)已知:如图,直y=2x+b交x轴于点B,交y轴于点C,点A为x轴正半轴上一点,AO=CO,△ABC的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
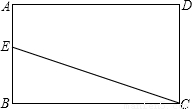
 如图有一个矩形花坛ABCD,有个别人贪图方便,从E点直插过去到C点,已知BE=7米,BC=24米,那么这些人以践踏花草为代价,仅仅是只少走了________米的路程.
如图有一个矩形花坛ABCD,有个别人贪图方便,从E点直插过去到C点,已知BE=7米,BC=24米,那么这些人以践踏花草为代价,仅仅是只少走了________米的路程.查看答案和解析>>
科目:初中数学 来源:《1.1-1.2 证明(二)》2009年水平测试C卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com