练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图，已知AB=A1B，A1C=A1A2，A2D=A2A3，A3E=A3A4，∠B=20°，则∠A4=
     
    度．
    分析：由∠B=20°根据三角形内角和公式可求得∠BA1A的度数，再根据等腰三角形的性质及三角形外角的性质找∠BA1A与∠A4的关系即可解答．
    解答：解：∵AB=A1B，∠B=20°，
    ∴∠A=∠BA1A=
    1
    2
    （180°-∠B）=
    1
    2
    （180°-20°）=80°
    ∵A1C=A1A2，A2D=A2A3，A3E=A3A4精英家教网
    ∴∠A1CD=∠A1A2C，
    ∵∠BA1A是△A1A2C的外角，
    ∴∠BA1A=2∠CA2A1=4∠DA3A2=8A4
    ∴∠A4=10°．
    故填10．
    点评：本题考查了三角形内角和定理，三角形外角与内角的关系及等腰三角形的性质的综合运用．充分利用外角找着∠BA1A与∠A4的关系是正确解答本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

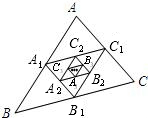    精英家教网如图，已知△ABC的周长为m，分别连接AB，BC，CA的中点A1，B1，C1得△A1B1C1，再连接A1B1，B1C1，C1A1的中点A2，B2，C2得△A2B2C2，再连接A2B2，B2C2，C2A2的中点A3，B3，C3得△A3B3C3，…，这样延续下去，最后得△AnBnCn．设△A1B1C1的周长为l1，△A2B2C2的周长为l2，△A3B3C3的周长为l3，…，△AnBnCn的周长为ln，则ln=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

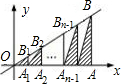    精英家教网如图，已知A（4，0），点A1、A2、…、An-1将线段OAn等分，点B1、B2、…、Bn-1、B在直线y=0.5x上，且A1B1∥A2B2∥…∥An-1Bn-1∥AB∥y轴．记△OA1B1、△A1A2B2、…、△An-2An-1Bn-1、△An-1AB的面积分别为S1、S2、…Sn-1、Sn．当n越来越大时，猜想S1+S2+…+Sn最近的常数是（　　）
    A、1B、2C、4D、8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，已知直角△ACB，AC=1，BC=
    		3
    ，过直角顶点C作CA1⊥AB，垂足为A1，再过A1作A1C1⊥BC，垂足为C1；过C1作C1A2⊥AB，垂足为A2，再过A2作A2C2⊥BC，垂足为C2；…，这样一直做下去，得到一组线段CA1，A1C1，C1A2，…，则第12条线段A6C6=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•五通桥区模拟）如图，已知∠MON=30°，AB⊥ON，垂足为点A，点B在射线OM上，AB=1cm，在射线ON上截取OA1=OB，过A1作A1B1∥AB，A1B1交射线OM于点B1，再在射线ON上截取OA2=OB1，过点A2作A2B2∥AB，A2B2交射线OM于点B2；…依次进行下去，则A1B1线段的长度为
    2
    		3
    3
    2
    		3
    3
    ，A10B10线段的长度为
    210
    		3
    3
    210
    		3
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

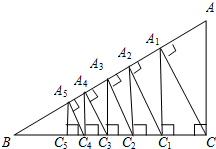
    （2012•德化县模拟）如图，已知直角三角形ABC中，∠ACB=90°，AC=1，BC=2，过点C作CA1⊥AB，垂足为A1，再过A1作A1C1⊥BC，垂足为C1；过C1作C1A2⊥AB，垂足为A2，再过A2作A2C2⊥BC，垂足为C2；…，这样一直做下去，得到了一组线段CA1，A1C1，C1A2，…，则第1条线段A1C=
    2
    		5
    5
    2
    		5
    5
    ，第2n条线段AnCn=
    （
    2
    		5
    5
    ）2n
    （
    2
    		5
    5
    ）2n
    ．

    查看答案和解析>>

    同步练习册答案