
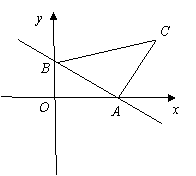
如图,一次函数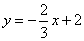 的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点C的坐标;
(2)在x轴上求一点P,使它到B、C两点的距离之和最小.
 |
解:(1)在一次函数y=﹣x+2中,
令x=0得:y=2;
令y=0,解得x=3,
则B的坐标是(0,2),A的坐标是(3,0).
如图,作CD⊥x轴于点D.
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO.
在△ABO与△CAD中,
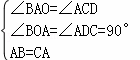 ,
,
∴△ABO≌△CAD(AAS),
∴OB=AD=2,OA=CD=3,OD=OA+AD=5.
则C的坐标是(5,3).
(2)B关于x轴的对称点的坐标是B′(0,﹣2),
设直线B′C的解析式是y=kx+b,
根据题意得: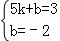 ,
,
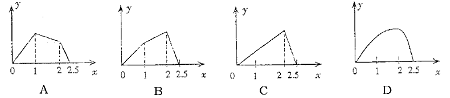
解得: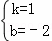 ,
,
∴直线B′C的解析式是y=x﹣2.
令y=0,解得:x=2,
则P的坐标是:(2,0).


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
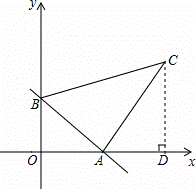
如图,点P按A→B→C→M的顺序在边长为1的正 方形边上运动,
方形边上运动,

 M是CD边上的中点.设点P经过的路程x为自变量,△APM的
M是CD边上的中点.设点P经过的路程x为自变量,△APM的
 面积为y,则函数y的大致图像是 ( )
面积为y,则函数y的大致图像是 ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解某校学生的身高情况,随机抽取该校若干名学生测量他们的身高,已知抽取的学生中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高分组表 女生身高频数分布表 男生身高频数分布直方图
|
|
|
请根据以上图表提供的信息,解答下列问题:
(1)在女生身高频数分布表中: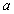 = ,
= ,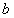 = ,
= ,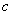 = ;
= ;
(2)补全男生身高频数分布直方图;
(3)已知该校共有女生400人,男生380人,请估计身高在165≤ <170之间的学生约有多少人.
<170之间的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c(a≠0)部分图像如图,图像过点(-1,0)对称轴为x=2,有下列结论
①4a+b=0 ②c+9a>3b ③8a+7b+2c<0 ④当x>-1,y随x的增大而增大
正确的结论有()
A 1 B 2 C 3 D 4

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com