

分析 (1)若点B在线段AC上的黄金分割点,且AB>BC,则$\frac{AB}{AC}$=$\frac{BC}{AB}$,设AB=x,则BC=2-x代入求值即可.
(2)①利用勾股定理画出$\sqrt{5}$,再在长为$\sqrt{5}$的线段上截取长为1的线段,剩余部分就是$\sqrt{5}-1$.
②根据配方法解该方程的根即可,作图与①雷同.
解答 解:(1)①设AB=x,则BC=2-x
∵点B在线段AC上的黄金分割点,且AB>BC,
∴$\frac{AB}{AC}$=$\frac{BC}{AB}$,
可列方程为:$\frac{x}{2}$=$\frac{2-x}{x}$,
解得:x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$,
∴AB的长为:-1+$\sqrt{5}$;
故答案为:$\frac{AB}{AC}$=$\frac{BC}{AB}$,$\frac{x}{2}$=$\frac{2-x}{x}$,x1=-1+$\sqrt{5}$,x2=-1-$\sqrt{5}$,-1+$\sqrt{5}$;
②作图见下图1:
(2)①证明:解关于x的方程x2+2mx=n2:
x2+2mx+m2=m2+n2
(x+m)2═m2+n2,
∵t是关于x的方程x2+2mx=n2的一正实数根,
∴(t+m)2=m2+n2;
②作图见下图
点评 本题考查了:黄金分割、解一元一次方程、勾股定理等知识点,解题的关键是掌握以上知识点的内涵及其应用方法.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
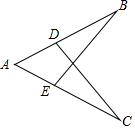 (1)如图,已知∠B=∠C,AD=AE,求证:BD=CE.
(1)如图,已知∠B=∠C,AD=AE,求证:BD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
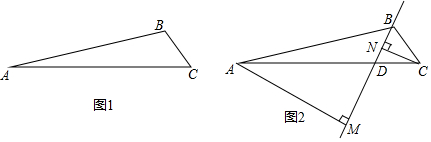
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com