

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:不详 题型:解答题
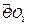 和
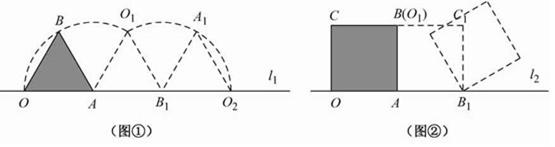
和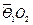 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧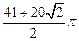 ?
?
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC. 的中点;
的中点; ,且AC=4,求CF的长.
,且AC=4,求CF的长.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
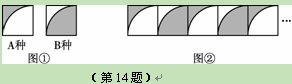
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
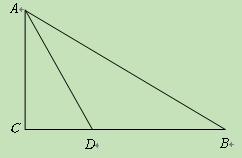
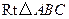 中,
中,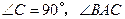 的角平分线
的角平分线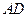 交
交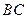 边于
边于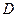 .
.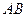 边上一点
边上一点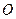 为圆心,过
为圆心,过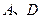 两点作
两点作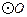 (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线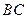 与
与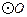 的位置关系,并说明理由;
的位置关系,并说明理由;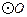 与
与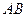 边的另一个交点为
边的另一个交点为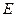 ,
,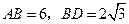 ,求线段
,求线段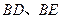 与劣弧
与劣弧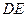 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和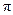 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为
为
 的中点,连接
的中点,连接 交
交 于点
于点 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 。
。
 是半圆
是半圆 的切线;
的切线; ,
, ,求
,求 的长。
的长。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com