
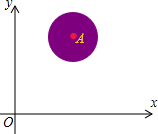
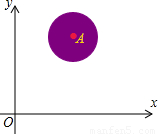
 如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为________ 时,X能由红变黑.
如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为________ 时,X能由红变黑. ≤b≤
≤b≤
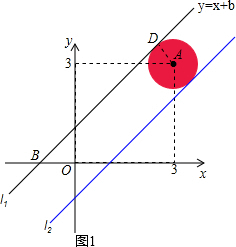 解法(一):如图所示1,当直线y=x+b与⊙A相切时,且在⊙A的上方时,则过点A作AD⊥l1于点D,AD=1.
解法(一):如图所示1,当直线y=x+b与⊙A相切时,且在⊙A的上方时,则过点A作AD⊥l1于点D,AD=1. =1,即
=1,即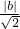 =1,
=1, ,或b=-
,或b=- (不合题意,舍去).
(不合题意,舍去). .
. ≤b≤
≤b≤ ;
; ≤b≤
≤b≤ .
.
 OE=
OE= .
. ,
, ≤b≤
≤b≤ ;
; ≤b≤
≤b≤ .
.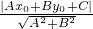 .解法(二)中利用了切线的性质、勾股定理等知识.
.解法(二)中利用了切线的性质、勾股定理等知识. 

科目:初中数学 来源: 题型:
 5、如图,有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲,其中,A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到区域甲时,甲由黑变白.甲能由黑变白,则b的取值范围为( )
5、如图,有一种动画程序,屏幕上正方形区域ABCD表示黑色物体甲,其中,A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y=2x+b发射信号,当信号遇到区域甲时,甲由黑变白.甲能由黑变白,则b的取值范围为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 12、如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为( )
12、如图,有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A(1,1),B(2,1),C(2,2),D(1,2),用信号枪沿直线y=-2x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围为( )查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为
如图,有一种Flash动画程序,屏幕上圆形区域表示红色小动物X,其中,A(3,3),⊙A的半径为1,用发射枪沿直线y=x+b发射子弹,当子弹遇到圆形区域X时,X就由红变黑.则b的取值范围为| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2012年江苏省淮安市中考数学模拟试卷(十)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com