
���� ��1���������䷽����Ǹ���������֤�����ɣ�
��������֤��������3x2-5x-1-��2x2-4x-7��=x2-x+6���䷽�õ���x-$\frac{1}{2}$��2+$\frac{23}{4}$��Ȼ����ݷǸ��������ʽ���֤����
��2���������������ߵĹ�ϵ����������֮�ʹ��ڵ����ߣ��������߶��е�����������Ӻ���������߶αȽϴ�С���Ƚϴ�С�ķ����루1��һ���������������߶��е�����������Ӻ��ڵ������߶Σ�����ж������߶ο���Ϊ�����ε������ߣ�
��� ��1����֤����2x2+4x+3=2��x+1��2+1��
�ߣ�x+1��2��0��
��2��x+1��2+1��0��
�������κ�ʵ��x������2x2+4x+3��0��
��֤����3x2-5x-1-��2x2-4x-7��=x2-x+6
=x2-x+$\frac{1}{4}$-$\frac{1}{4}$+6
=��x-$\frac{1}{2}$��2+$\frac{23}{4}$��
�ߣ�x-$\frac{1}{2}$��2��0��
�ࣨx-$\frac{1}{2}$��2+$\frac{23}{4}$��0��
��3x2-5x-1��2x2-4x-7��
��2���⣺��m2-2m-3+m2-4-��m2+2m-3��=m2-4m-4=��m-2��2-8��
��m��5��
�ࣨm-2��2-8��0����m2-2m-3+m2-4��m2+2m-3��
��m2-2m-3+m2+2m-3-��m2-4��=m2-2��
��m��5��
��m2-2����m2-2m-3+m2+2m-3��m2-4��
��m2-4+m2+2m-3-��m2-2m-3��=m2+4m-4=��m+2��2-8��
��m��5��
�ࣨm+2��2-8��0����m2-4+m2+2m-3��m2-2m-3��
�������߶�m2-2m-3��m2-4��m2+2m-3����Ϊ�����ε������ߣ�
���� ���⿼�����䷽����Ӧ�ã����䷽����һԪ���η��̣������䷽�����������ʽ��һ����ȫƽ��ʽʱ������ĸϵ����ֵ����������ʽ����ȫƽ��ʽ����������һ����ϵ��һ���ƽ������Ҳ�����˷Ǹ��������ʺ����������ߵĹ�ϵ��


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
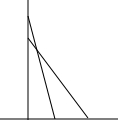 һ�����ݳ�25m����ͼ����б����һ��ǽ�ϣ����ݵ���ǽ7m
һ�����ݳ�25m����ͼ����б����һ��ǽ�ϣ����ݵ���ǽ7m�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����һ��б��AB��12cm����B=60������dz�ABC����ʱ�뷽���Ƶ�C��ת90�㣬����CB����ƽ�ƣ�ʹ��B��պ��䵽б��AB�ϣ����A��B��C����ƽ�Ƶľ��룮
��ͼ����һ��б��AB��12cm����B=60������dz�ABC����ʱ�뷽���Ƶ�C��ת90�㣬����CB����ƽ�ƣ�ʹ��B��պ��䵽б��AB�ϣ����A��B��C����ƽ�Ƶľ��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
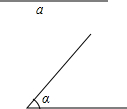 ��ͼ�⣺
��ͼ�⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ������x�� | 60��x��80 | 80��x��100 | 100��x��120 | 120��x��140 | 140��x��160 | 160��x��180 | 180��x��200 |
| Ƶ���������� | 2 | 4 | 21 | 13 | 8 | 4 | 1 |
| A�� | ���8������20 | B�� | ���20������7 | C�� | ���7������20 | D�� | ���40������7 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com