
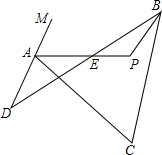
 如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P=________.
如图,已知AP平分∠CAM,BP平分∠CBD,∠C=62°,∠D=30°,则∠P=________. (180°-∠C-∠CGB),∠PEB=180°-∠D-∠DAE,由三角形外角的性质可知,∠EAG=
(180°-∠C-∠CGB),∠PEB=180°-∠D-∠DAE,由三角形外角的性质可知,∠EAG= (180°-∠DAG)再把三式联立即可得出结论.
(180°-∠DAG)再把三式联立即可得出结论.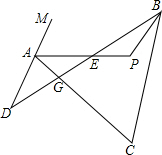 解:∵∠P=180°-∠PBE-∠PEB,
解:∵∠P=180°-∠PBE-∠PEB, (180°-∠C-∠CGB)①,
(180°-∠C-∠CGB)①, (180°-∠DAG)③
(180°-∠DAG)③ (180°-∠C-∠CGB)-∠PEB
(180°-∠C-∠CGB)-∠PEB ∠C+
∠C+ ∠CGB-(180°-∠D-∠DAE)
∠CGB-(180°-∠D-∠DAE) ∠C+
∠C+ ∠CGB-90°+∠D+(∠DAG+
∠CGB-90°+∠D+(∠DAG+ ∠CAM)
∠CAM) ∠C+
∠C+ ∠CGB-90°+∠D+(180°-∠D-∠DGA)+
∠CGB-90°+∠D+(180°-∠D-∠DGA)+ (∠D+∠DGA)
(∠D+∠DGA) ∠C+
∠C+ ∠D
∠D ×62°+
×62°+ ×30°
×30°

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2004年重庆市中考数学模拟试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com