
 =90°,客轮速度是货轮速度的2倍.
=90°,客轮速度是货轮速度的2倍.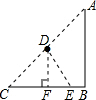 解:(1)B
解:(1)B AB=100,EF=400-100-2x,
AB=100,EF=400-100-2x,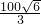 ,
,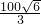 >100
>100 (舍去),
(舍去),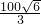 .
.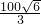 )海里.
)海里. AB=100,EF=400-100-2x,在Rt△DFE中,DE2=DF2+EF2,得x2=1002+(300-2x)2解方程求解即可.
AB=100,EF=400-100-2x,在Rt△DFE中,DE2=DF2+EF2,得x2=1002+(300-2x)2解方程求解即可.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
 =90°,客轮速度是货轮速度的2倍.
=90°,客轮速度是货轮速度的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:
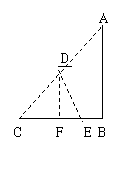
如图,客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮.两船同时起航,并同时到达折线A-B-C上的某点E处.已知AB=BC=200海里,∠ABC=90°,客轮速度是货轮速度的2倍.
(1)选择:两船相遇之处E点( )
(A)在线段AB上;(B)在线段BC上;(C)可以在线段AB上,也可以在线段BC上;
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,客轮沿折线A-B-C从A出发经B再到C匀速航行,货轮从AC的中点D出发沿某一方向匀速直线航行,将一批物品送达客轮。两船同时起航,并同时到达折线A-B-C的某点E处,已知AB=BC=200海里,∠ABC=90°,客轮速度是货轮速度的2倍。
(1)选择:两船相遇之处E点( )。
A、在线段AB上 B、在线段BC上 C、可以在线段AB上,也可以在线段BC上
(2)求货轮从出发到两船相遇共航行了多少海里?(结果保留根号)。

查看答案和解析>>
科目:初中数学 来源:2009-2010学年九年级(上)数学期末复习题(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com