

分析 (1)根据三角函数得出AB的长度解答即可;
(2)过点P作PD⊥OB,根据三角形的面积公式和二次函数的最值解答即可;
(3)根据直角三角形的性质和等腰三角形的性质进行解答即可.
解答 解:(1)∵Rt△AOB中,OA=3,sinB=$\frac{3}{5}$,
∴AB=5,
∵设运动的时间为t,点P从点B出发,沿BA以a单位/秒的速度向点A运动,
∴AP=5-at,
故答案为:5-at;
(2)如图①: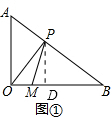
过点P作PD⊥OB,在Rt△PDB中,PB=t,sinB=$\frac{3}{5}$,
∴PD=$\frac{3}{5}t$,OM=4-t,
∴$S=\frac{1}{2}(4-t)•\frac{3}{5}t=-\frac{3}{10}(t-2)^{2}+\frac{6}{5}$,
∵0≤t≤4,
∴当t=2时,${S}_{最大值}=\frac{6}{5}$;
(3)假设存在,
①若∠PMB=90°,如图②: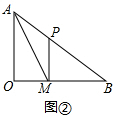
∵PA=PM,
在Rt△PMB中,PB=at,sinB=$\frac{3}{5}$,
∴PM=$\frac{3}{5}$at,MB=$\frac{4}{5}$at,
根据题意可得:$\left\{\begin{array}{l}{5-at=\frac{3}{5}at}\\{\frac{4}{5}at=t}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{5}{4}}\\{t=\frac{5}{2}}\end{array}\right.$,符合题意;
②若∠MPB=90°,如图③,则∠APM=90°,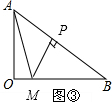
∴PA=PM,
在Rt△PMB中,PB=at,sinB=$\frac{3}{5}$,
∴$PM=\frac{3}{4}at,MB=\frac{5}{4}at$,
根据题意可得:$\left\{\begin{array}{l}{5-at=\frac{3}{4}at}\\{\frac{5}{4}at=t}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{4}{5}}\\{t=\frac{25}{7}}\end{array}\right.$,符合题意,
∴存在某时刻,使得△PMB为直角三角形且△PMA是等腰三角形,此时$\left\{\begin{array}{l}{{a}_{1}=\frac{5}{4}}\\{{t}_{1}=\frac{5}{2}}\end{array}\right.或\left\{\begin{array}{l}{{a}_{2}=\frac{4}{5}}\\{{t}_{2}=\frac{25}{7}}\end{array}\right.$.
点评 此题主要考查了三角形综合题,关键是根据三角函数得出AB的长度,同时根据直角三角形的性质和等腰三角形的性质解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
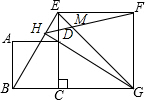 如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.
如图,正方形ABCD的顶点D在正方形ECGF的边EC上,顶点B在GC的延长线上,连接EG、BE,∠EGC的平分线GH过点D交BE于H,连接HF交EG于M,则$\frac{MG}{ME}$的值为$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (4,1) | B. | (5,1) | C. | (6,1) | D. | (7,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com