
 (2013•梅列区模拟)汽车超速行驶是引发交通事故的主要原因,在社会实践活动期间,高小明和同学尝试用自己所学的知识进行检测公路上行驶的车速,检测方案如下示意图;在距离检测公路100米的观测点P处,观测到一辆小轿车正位于观测点北偏西60°的A处由西向东匀速行驶,经过4秒到达位于观测点北偏西45°的B处.
(2013•梅列区模拟)汽车超速行驶是引发交通事故的主要原因,在社会实践活动期间,高小明和同学尝试用自己所学的知识进行检测公路上行驶的车速,检测方案如下示意图;在距离检测公路100米的观测点P处,观测到一辆小轿车正位于观测点北偏西60°的A处由西向东匀速行驶,经过4秒到达位于观测点北偏西45°的B处.| 2 |
| 3 |
| 3 |
| 3 |
100(
| ||
| 4 |
| 3 |
| 60000 |
| 3600 |


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
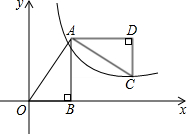 (2013•梅列区模拟)如图,△AOB在平面直角坐标系中,OB在x轴上,∠B=90°,点A的坐标为(2,3),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=
(2013•梅列区模拟)如图,△AOB在平面直角坐标系中,OB在x轴上,∠B=90°,点A的坐标为(2,3),将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com