
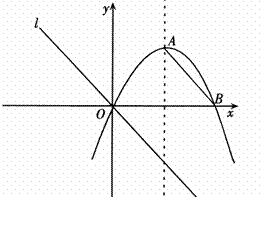
如图13,对称轴为![]() 的抛物线
的抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() 、
、![]() .
.
(1)求抛物线的解析式,并求出顶点![]() 的坐标;
的坐标;
(2)连结AB,把AB所在的直线平移,使它经过原点O,得到直线![]() .点P是
.点P是![]() 上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为![]() ,当0<S≤18时,求
,当0<S≤18时,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,当![]() 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点![]() ,使△
,使△![]() 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 |
(1)∵点B与O(0,0)关于x=3对称,
∴点B坐标为(6,0).
将点B坐标代入![]() 得:
得:
36![]() +12=0,
+12=0,
∴![]() =
=![]() .
.
∴抛物线解析式为![]() .…………………………2分
.…………………………2分
当![]() =3时,
=3时,![]() ,
,
∴顶点A坐标为(3,3). …………………………1分
(说明:可用对称轴为![]() ,求
,求![]() 值,用顶点式求顶点A坐标.)
值,用顶点式求顶点A坐标.)
#*(2)设直线AB解析式为y=kx+b.
∵A(3,3),B(6,0),
∴![]() 解得
解得![]() , ∴
, ∴![]() .-
.-
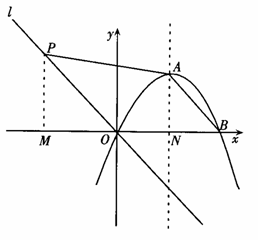 ∵直线
∵直线![]() ∥AB且过点O,
∥AB且过点O,
∴直线![]() 解析式为
解析式为![]() .
.
∵点![]() 是
是![]() 上一动点且横坐标为
上一动点且横坐标为![]() ,
,
∴点![]() 坐标为(
坐标为(![]() ).
).
当![]() 在第四象限时(t>0),
在第四象限时(t>0),
![]()
=12×6×3+![]() ×6×
×6×![]()
=9+3![]() .
.
∵0<S≤18
∴0<9+3![]() ≤18,
≤18,
∴-3<![]() ≤3.
≤3.
又![]() >0,
>0,
当![]() 在第二象限时(
在第二象限时(![]() <0),
<0),
作PM⊥![]() 轴于M,设对称轴与
轴于M,设对称轴与![]() 轴交点为N. 则
轴交点为N. 则
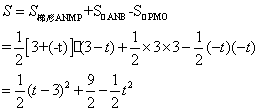
=-3![]() +9.
+9.
∵0<S≤18,
∴0<-3![]() +9≤18,
+9≤18,
∴-3≤![]() <3.
<3.
又![]() <0,
<0,
∴-3≤![]() <0 ------------------2分
<0 ------------------2分
∴t的取值范围是-3≤![]() <0或0<
<0或0<![]() ≤3.5----------------1分
≤3.5----------------1分
*(3)存在,点![]() 坐标为(3,3)或(6,0)或(-3,-9)
坐标为(3,3)或(6,0)或(-3,-9)


科目:初中数学 来源: 题型:
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
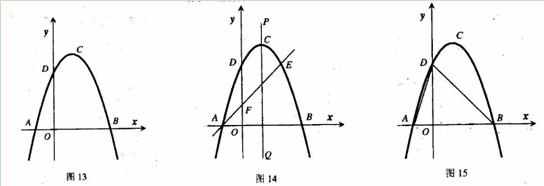
(9分)如图13,抛物线y=ax2+bx+c(a≠0)的顶点为(1,4),交x轴于A、B,交y轴于D,其中B点的坐标为(3,0)
(1)求抛物线的解析式
(2)如图14,过点A的直线与抛物线交于点E,交y轴于点F,其中E点的横坐标为2,若直线PQ为抛物线的对称轴,点G为PQ上一动点,则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
(3)如图15,抛物线上是否存在一点T,过点T作x的垂线,垂足为M,过点M作直线MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD,若存在,求出点T的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(云南红河) 题型:解答题
如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com