
| A. | 0 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{7}$ |
分析 △ABC中,|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=1,故三角形是边长为1的等边三角形,AB,BC两向量的夹角是60°,由平方法求|$\overrightarrow{AC}$+2$\overrightarrow{BC}$|的值即可.
解答 解:∵在△ABC中,|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|=|$\overrightarrow{BC}$|=1,
∴△ABC是边长为1的等边三角形,
∴AB,BC两向量的夹角是60°,
∴|$\overrightarrow{AC}$+2$\overrightarrow{BC}$|=$\sqrt{|\overrightarrow{AC}{|}^{2}+4|\overrightarrow{BC}{|}^{2}+4|\overrightarrow{AC}|•|\overrightarrow{BC}|cos60°}$=$\sqrt{1+4+4×1×1×\frac{1}{2}}$=$\sqrt{7}$.
故选:D.
点评 本题考点是向量的模,求向量的模的方法一般采取平方的方法,本题中把向量的模进行了恒等变形得到了平方的形式,此方式是求向量模最常用的技巧.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
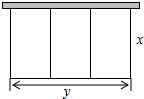 如图所示,猪舍三间,它们的形状是一排大小相等的三个矩形,一面利用旧墙(旧墙长12m),包括隔墙在内的其它各墙均用木料,已知现有木料可围24m的墙,设整个猪舍的长为ym,宽为xm,则y与x的函数关系式为y=24-4x,自变量x的取值范围是3≤x<6.
如图所示,猪舍三间,它们的形状是一排大小相等的三个矩形,一面利用旧墙(旧墙长12m),包括隔墙在内的其它各墙均用木料,已知现有木料可围24m的墙,设整个猪舍的长为ym,宽为xm,则y与x的函数关系式为y=24-4x,自变量x的取值范围是3≤x<6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com