
如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?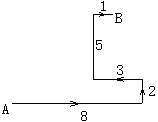
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
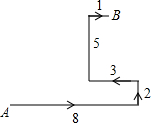 如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?
如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?查看答案和解析>>
科目:初中数学 来源:2014届湖北省八年级下学期期中考试数学试卷(解析版) 题型:解答题
如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?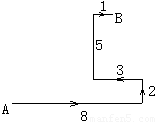
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
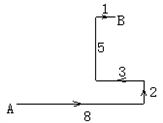
 如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?
如图所示,某人到一个荒岛上去探宝,在A处登陆后,往东走8km,又往北走2km,遇到障碍后又往西走3km,再折向北方走到5km处往东一拐,仅1km就找到了宝藏,问:登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少?查看答案和解析>>
科目:初中数学 来源:专项题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com