
 如图,△ABC中,AB=BC,将△ABC沿直线BC平移到△DCE(使B与C重合),连接BD,求∠BDE的度数.
如图,△ABC中,AB=BC,将△ABC沿直线BC平移到△DCE(使B与C重合),连接BD,求∠BDE的度数.

科目:初中数学 来源: 题型:
 某同学一家三口随旅游团去九寨沟旅游,该同学把旅途费用支出情况制成了如图的统计图:
某同学一家三口随旅游团去九寨沟旅游,该同学把旅途费用支出情况制成了如图的统计图:| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
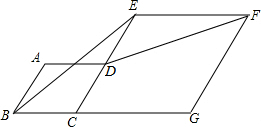 如图,菱形ABCD的边CD在菱形ECGF的边CE上,且D是CE中点.连接BE,DF.
如图,菱形ABCD的边CD在菱形ECGF的边CE上,且D是CE中点.连接BE,DF.查看答案和解析>>
科目:初中数学 来源: 题型:
 将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):| 数据段 | 频数 | 频率 |
| 30~40 | 10 | 0.05 |
| 40~50 | 36 | a |
| 50~60 | b | 0.39 |
| 60~70 | c | d |
| 70~80 | 20 | 0.10 |
| 总计 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com