
分析 (1)若一元二次方程有两实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,求出m的取值范围;
(2)由x12-x22=0得x1+x2=0或x1-x2=0;当x1+x2=0时,运用两根关系可以得到-2m-1=0或方程有两个相等的实根,据此即可求得m的值
解答 解:(1)∵方程x2+(2m-1)+m2=0有两个实数根x1和x2,
∴△=(2m-1)2-4m2≥0,
解得:m≤$\frac{1}{4}$;
(2)由两根关系,得:x1+x2=-(2m-1),x1•x2=m2,
由x12-x22=0得(x1+x2)(x1-x2)=0,
若x1+x2=0,即-(2m-1)=0,解得m=$\frac{1}{2}$,
∵$\frac{1}{2}$>$\frac{1}{4}$,
∴m=$\frac{1}{2}$不合题意,舍去,
若x1-x2=0,即x1=x2
∴△=0,由(1)知m=$\frac{1}{4}$,
故当x12-x22=0时,m=$\frac{1}{4}$.
点评 本题考查了一元二次方程根的判别式及根与系数关系,利用两根关系得出的结果必须满足△≥0及熟练掌握韦达定理是关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知关于x的一次函数y=kx+4的图象经过点(1,2).
已知关于x的一次函数y=kx+4的图象经过点(1,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
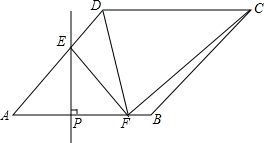 如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一个动点,过点P作PE⊥AB交直线AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=$\sqrt{2}$或2+$\sqrt{2}$..
如图,在菱形ABCD中,∠DAB=45°,AB=4,点P为线段AB上一个动点,过点P作PE⊥AB交直线AD于点E,沿PE将∠A折叠,点A的对称点为点F,连接EF、DF、GF,当△CDF为直角三角形时,AP=$\sqrt{2}$或2+$\sqrt{2}$..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com