数学问题:计算$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+-+\frac{1}{{m}^{n}}$*(其中m.n都是正整数.且m≥2.n≥1)探究问题:为解决上面的数字问题.我们运用数形结合的思想方法.通过不断地分割一个面积为1的正方形.把数量关系和几何图形巧妙地结合起来.并采取一般问题特殊化的策略来� 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

10．数学问题：计算$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+…+\frac{1}{{m}^{n}}$*（其中m，n都是正整数，且m≥2，n≥1）
探究问题：为解决上面的数字问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$
第1次分割，把正方形的面积二等分，其中阴影部分的面积为$\frac{1}{2}$；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为$\frac{1}{2}+\frac{1}{{2}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$，最后空白部分的面积是$\frac{1}{{2}^{n}}$．
根据第n次分割图可得等式：$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$．

探究二：计算$\frac{1}{3}$+$\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}}$．
第1次分割，把正方形的面积三等分，其中阴影部分的面积为$\frac{2}{3}$；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为$\frac{2}{3}+\frac{2}{{3}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为$\frac{2}{3}$+$\frac{2}{{3}^{2}}+\frac{2}{{3}^{3}}+…+\frac{2}{{3}^{n}}$，最后空白部分的面积是$\frac{1}{{3}^{n}}$．
根据第n次分割图可得等式：$\frac{2}{3}$+$\frac{2}{{3}^{2}}+\frac{2}{{3}^{3}}+…+\frac{2}{{3}^{n}}$=1-$\frac{1}{{3}^{n}}$．
两边同除以2，得$\frac{1}{3}$+$\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}}$=$\frac{1}{2}$$-\frac{1}{2×{3}^{n}}$\

探究三：计算$\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+..+\frac{1}{{4}^{n}}$．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）

解决问题：根据前面探究结果：
$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$
$\frac{1}{3}$+$\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}}$=$\frac{1}{2}$$-\frac{1}{2×{3}^{n}}$
$\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+..+\frac{1}{{4}^{n}}$=$\frac{1}{3}$-$\frac{1}{3×{4}^{n}}$．
…
推出：$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+…+\frac{1}{{m}^{n}}$=$\frac{1}{m-1}$-$\frac{1}{（m-1）{m}^{n}}$．（只填空，其中m、n都是正整数，且m≥2，n≥1）
拓广应用：计算$\frac{5-1}{5}+\frac{{5}^{2}-1}{{5}^{2}}+\frac{{5}^{3}-1}{{5}^{3}}+…+\frac{{5}^{n}-1}{{5}^{n}}$．

分析 ①探究三：根据探究二进行分割方法依次进行分割，然后表示出阴暗部分的面积，再除以3即可；
②推出：根据探究二进行分割方法依次进行分割，然后表示出阴暗部分的面积，再除以m-1即可；
③拓广应用：先把每一个分数化成1减去一个分数，然后应用公式计算．

解答解：探究三：计算$\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+..+\frac{1}{{4}^{n}}$．
第1次分割，把正方形的面积四等分，其中阴影部分的面积为$\frac{3}{4}$；
第2次分割，把上次分割图中空白部分的面积继续四等分，阴影部分的面积之和为$\frac{3}{4}+\frac{3}{{4}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续四等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后四等分，所有阴影部分的面积之和为$\frac{2}{3}$+$\frac{3}{4}+\frac{3}{{4}^{2}}+\frac{3}{{4}^{3}}+…+\frac{3}{{4}^{n}}$，最后空白部分的面积是$\frac{1}{{4}^{n}}$；
根据第n次分割图可得等式：$\frac{3}{4}+\frac{3}{{4}^{2}}+\frac{3}{{4}^{3}}+…+\frac{3}{{4}^{n}}$=1-$\frac{1}{{4}^{n}}$；
两边同除以3，得$\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+..+\frac{1}{{4}^{n}}$=$\frac{1}{3}$-$\frac{1}{3×{4}^{n}}$．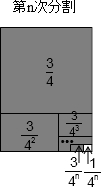

推出：$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+…+\frac{1}{{m}^{n}}$，
第1次分割，把正方形的面积m等分，其中阴影部分的面积为$\frac{m-1}{m}$，
第2次分割，把上次分割图中空白部分的面积继续m等分，阴影部分的面积之和为$\frac{m-1}{m}+\frac{m-1}{{m}^{2}}$，
第3次分割，把上次分割图中空白部分的面积继续m等分，…，
…
第n次分割，把上次分割图中空白部分的面积最后m等分，所有阴影部分的面积之和为$\frac{m-1}{m}+\frac{m-1}{{m}^{2}}+\frac{m-1}{{m}^{3}}+…+\frac{m-1}{{m}^{n}}$，最后空白部分的面积是$\frac{1}{{m}^{n}}$，
根据第n次分割图可得等式：$\frac{m-1}{m}+\frac{m-1}{{m}^{2}}+\frac{m-1}{{m}^{3}}+…+\frac{m-1}{{m}^{n}}$=1-$\frac{1}{{m}^{n}}$，
两边同除以m-1，得$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+…+\frac{1}{{m}^{n}}$=$\frac{1}{m-1}$-$\frac{1}{（m-1）{m}^{n}}$；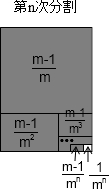

故答案为：$\frac{1}{3}$-$\frac{1}{3×{4}^{n}}$，$\frac{1}{m-1}$-$\frac{1}{（m-1）{m}^{n}}$；
应用：计算$\frac{5-1}{5}+\frac{{5}^{2}-1}{{5}^{2}}+\frac{{5}^{3}-1}{{5}^{3}}+…+\frac{{5}^{n}-1}{{5}^{n}}$，
=1-$\frac{1}{5}$+1-$\frac{1}{{5}^{2}}$+1-$\frac{1}{{5}^{3}}$+…+1-$\frac{1}{{5}^{n}}$，
=n-（$\frac{1}{4}$-$\frac{1}{4×{5}^{n}}$），
=n-$\frac{1}{4}$+$\frac{1}{4×{5}^{n}}$．

点评本题一方面考查了数字、图形的变化规律，同时还考查了应用与设计作图，读懂题目信息，理解分割的方法是关键，运用面积法将代数式的和相加并计算出结果．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

20．若定义a•b=ab+a+b，从左到右依次计算x=1•2•3…（n-1）•n，则满足x＞2016的最小正整数n是（　　）

A．

B．

C．

D．

查看答案和解析>>