
分析 根据平方差公式(a+b)(a-b)=a2-b2即可求解.
解答 解:(-b-$\frac{1}{2}$)(-b+$\frac{1}{2}$)=$\frac{1}{4}-{b}^{2}$;($\frac{3}{4}$m-$\frac{1}{2}$n)($\frac{3}{4}$m+$\frac{1}{2}$n)=$\frac{9}{16}{m}^{2}-\frac{1}{4}{n}^{2}$,
故答案为:$\frac{1}{4}-{b}^{2}$;$\frac{9}{16}{m}^{2}-\frac{1}{4}{n}^{2}$
点评 本题考查了平方差公式,运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
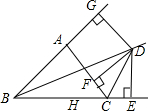 如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是DE=DF=DG.
如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是DE=DF=DG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com