
分析 (1)根据方程有两个不相等的实数根结合根的判别式即可得出△=-4m+4>0,解不等式即可得出m的取值范围;
(2)结合(1)取m=0,将其代入原方程中,利用分解因式法即可求出方程的解;
(3)根据根与系数的关系可得出x1+x2=-2(m-2)、x1•x2=m2-3m+3,结合${x_1}^2$$+{x_2}^2=6$,即可求出m的值,再根据△≥0可求出m的取值范围,由此即可确定m的值.
解答 解:(1)∵方程x2+2(m-2)x+m2-3m+3=0有两个不相等的实数,
∴△=[2(m-2)]2-4(m2-3m+3)=-4m+4>0,
解得:m<1.
∴方程有两个不相等的实数时,m的取值范围为m<1.
(2)取m=0,当m=0时,原方程为x2-4x+3=0,
解得:x1=1,x2=3.
(3)∵方程x2+2(m-2)x+m2-3m+3=0的两根为x1,x2,
∴x1+x2=-2(m-2),x1•x2=m2-3m+3,
∴${{x}_{1}}^{2}$+${{x}_{2}}^{2}$=$({x}_{1}+{x}_{2})^{2}$-2x1•x2=[-2(m-2)]2-2(m2-3m+3)=2m2-10m+10=6,
即m2-5m+2=0,
解之得:m1=$\frac{5-\sqrt{17}}{2}$,m2=$\frac{5+\sqrt{17}}{2}$.
∵△=[2(m-2)]2-4(m2-3m+3)=-4m+4≥0,
∴m≤1,
∴m=$\frac{5-\sqrt{17}}{2}$.
点评 本题考查了根的判别式以及根与系数的关系,熟练掌握“当方程有两个不相等的实数根时,△>0;当方程有实数根时,△≥0”是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
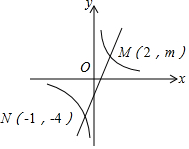 如图所示,反比例函数y=$\frac{k}{x}$(k≠0)的图象与一次函数y=ax+b的图象交于M(2,m),N(-1,-4)两点.
如图所示,反比例函数y=$\frac{k}{x}$(k≠0)的图象与一次函数y=ax+b的图象交于M(2,m),N(-1,-4)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≥$\frac{1}{3}$ | B. | m≤$\frac{1}{3}$ | C. | m<$\frac{1}{3}$ | D. | m>$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 候选人 | 教学技能考核成绩 | 专业知识考核成绩 |
| 甲 | 85 | 92 |
| 乙 | 91 | 85 |
| 丙 | 80 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4 (速度单位:单位长度/秒).
动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4 (速度单位:单位长度/秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
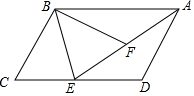 已知:如图,在?ABCD中,BE⊥CD,垂足为E,连接AE,F为AE上一点,∠BFE=∠C.
已知:如图,在?ABCD中,BE⊥CD,垂足为E,连接AE,F为AE上一点,∠BFE=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com