Question

方程2x（kx-4）-x²+6=0没有实数根，则k最小整数的值是（ ）
A．-1
B．2
C．3
D．4

Answer 1

【答案】分析：先把方程变形为关于x的一元二次方程的一般形式：（2k-1）x²-8x+6=0，要方程无实数根，则△=8²-4×6（2k-1）＜0，
解不等式，并求出满足条件的最小整数k．
解答：解：方程变形一般形式：（2k-1）x²-8x+6=0，
∵方程2x（kx-4）-x²+6=0没有实数根，
∴△=8²-4×6（2k-1）＜0，解得k＞，
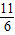
所以满足条件的最小整数k=2．
故选B．
点评：本题考查了一元二次方程ax²+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．