
【题目】风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)
【答案】解:如图,作BE⊥DH于点E,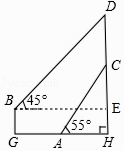
则GH=BE、BG=EH=10,
设AH=x,则BE=GH=GA+AH=43+x,
在Rt△ACH中,CH=AHtan∠CAH=tan55°x,
∴CE=CH﹣EH=tan55°x﹣10,
∵∠DBE=45°,
∴BE=DE=CE+DC,即43+x=tan55°x﹣10+35,
解得:x≈45,
∴CH=tan55°x=1.4×45=63,
答:塔杆CH的高为63米
【解析】作BE⊥DH,知GH=BE、BG=EH=10,设AH=x,则BE=GH=43+x,由CH=AHtan∠CAH=tan55°x知CE=CH﹣EH=tan55°x﹣10,根据BE=DE可得关于x的方程,解之可得.
【考点精析】掌握关于仰角俯角问题是解答本题的根本,需要知道仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
(1)试说明DF是⊙O的切线;
(2)若AC=3AE=6,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开放以下体育课外活动项目:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图(1),图(2)), 
请回答下列问题:
(1)这次被调查的学生共有人;
(2)请你将条形统计图补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE. 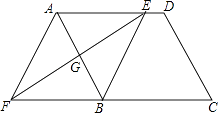
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB<BC,E为CD边的中点,将△ADE绕点E顺时针旋转180°,点D的对应点为C,点A的对应点为F,过点E作ME⊥AF交BC于点M,连接AM、BD交于点N,现有下列结论: ①AM=AD+MC;②AM=DE+BM;③DE2=ADCM;④点N为△ABM的外心.其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2 , l1、l2之间的距离为8,点P到直线l1的距离为6,点Q到直线l2的距离为4,PQ=4 ![]() ,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2 , 且PA+AB+BQ最小,此时PA+BQ= .
,在直线l1上有一动点A,直线l2上有一动点B,满足AB⊥l2 , 且PA+AB+BQ最小,此时PA+BQ= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气频发,市场上防护口罩出现热销.某药店准备购进一批口罩,已知1个A型口罩和3个B型口罩共需26元;3个A型口罩和2个B型口罩共需29元.
(1)求一个A型口罩和一个B型口罩的售价各是多少元?
(2)药店准备购进这两种型号的口罩共50个,其中A型口罩数量不少于35个,且不多于B型口罩的3倍,有哪几种购买方案,哪种方案最省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com