练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在海上观察所A，我边防海警发现正北6km的B处有一可疑船只正在向东方向8km的C处行驶．我边防海警即刻派船前往C处拦截．若可疑船只的行驶速度为40km/h，则我边防海警船的速度为多少时，才能恰好在C处将可疑船只截住？

    解：∵AB=6，BC=8
    ∴AC==10km，
    ∵可疑船只的行驶速度为40km/h，
    ∴可疑船只的行驶时间为8÷40=0.2小时，
    ∴我边防海警船的速度为10÷0.2=50km/小时，
    ∴我边防海警船的速度为50km/h时，才能恰好在C处将可疑船只截住．
    分析：首先利用勾股定理求得线段AC的长，然后利用行驶时间相等求得边防海警船的速度．
    点评：本题考查了勾股定理在实际生活中的应用，本题中正确的找到OB，AB的等量关系，并且根据该等量关系在直角△OAB中求解是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，在海上观察所A，我边防海警发现正北6km的B处有一可疑船只正在向东方向8km的C处行驶．我边防海警即刻派船前往C处拦截．若可疑船只的行驶速度为40km/h，则我边防海警船的速度为多少时，才能恰好在C处将可疑船只截住？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

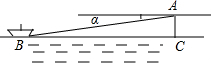    如图所示，在某海岛上的观察所A发现海上某船只B并测得其俯角α=8°14′，已知观察所A的标高（当水位为0m时的高度）为43.74m，当时水位为+2.63m，求观察所A到船只B的水平距离BC．（精确到1m）

    查看答案和解析>>

    同步练习册答案