
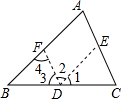
 已知:△ABC,求证:∠A+∠B+∠C=180°.(证明方法有多种)小明的证法如下:(请你将小明的证法补充完整,并在括号内填入推理的根据)
已知:△ABC,求证:∠A+∠B+∠C=180°.(证明方法有多种)小明的证法如下:(请你将小明的证法补充完整,并在括号内填入推理的根据)分析 根据平行线的性质得到∠1=∠B,∠2=∠DEC,∠3=∠C,∠4=∠A,等量代换得到∠2=∠A,根据平角的定义得到∠1+∠2+∠3=180°,等量代换即可得到结论.
解答 证明:在BC边上任取一点D,作DE∥BA交AC于E、DF∥CA交AB于F.
∵DE∥BA,
∴∠1=∠B,(两直线平行,同位角相等)
∠2=∠DEC.(两直线平行,内错角相等)
∵DF∥CA,
∴∠3=∠C,∠4=∠A.(两直线平行,同位角相等)
∴∠2=∠A,(等量代换)
又∵∠1+∠2+∠3=180°,(平角的定义)
∴∠A+∠B+∠C=180°.(等量代换)
故答案为:B,两直线平行,同位角相等,DEC,两直线平行,内错角相等,C,A,两直线平行,同位角相等,A,等量代换,平角的定义,等量代换.
点评 本题考查了平行线性质,主要考查学生的推理能力,根据题意作出辅助线,构造出平行线是解答此题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
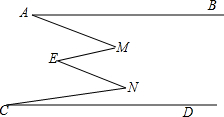 如图,AB∥CD,则下列结论正确的是( )
如图,AB∥CD,则下列结论正确的是( )| A. | ∠M+∠N=∠A+∠E+∠C | B. | ∠M+∠N<∠A+∠E+∠C | C. | ∠M=∠N | D. | ∠E=∠A+∠C |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
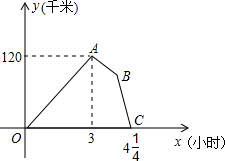 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后,卸完物品再另装货物共用45min,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示.
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后,卸完物品再另装货物共用45min,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com