
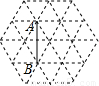
 如图,组成虚线网格的每个小正三角形的边长都为1,若有格点(小正三角形的顶点)C,使△ABC为等腰三角形,那么这样的C点共有________个.
如图,组成虚线网格的每个小正三角形的边长都为1,若有格点(小正三角形的顶点)C,使△ABC为等腰三角形,那么这样的C点共有________个. 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:

| 5 |
| 5 |
 形纸板剪拼成一个大正方形,要求剪两刀,画出剪拼的痕迹.
形纸板剪拼成一个大正方形,要求剪两刀,画出剪拼的痕迹.查看答案和解析>>
科目:初中数学 来源:2013届江苏泰兴济川中学八年级上期期末考试数学试卷(解析版) 题型:解答题
如图1,将由5个边长为1的小正方形组成的十字形纸板沿虚线剪拼成一个大正方形,需剪4
刀。

(1) 思考发现:大正方形的面积等于5个小正方形的面积和,大正方形的边长等于_______。
(2) 实践操作:如图2,将网格中5个边长为1的小正方形组成的图形纸板剪拼成一个大正方形,要求剪
两刀,画出剪拼的痕迹。
(3) 智力开发:将网格中的5个边长为1的正方形组成的十字形纸板,要求只剪2刀也拼成一个大正方形。
在图中用虚线画出剪拼的痕迹。
查看答案和解析>>
科目:初中数学 来源:2009年江苏省连云港市中考数学模拟试卷(二)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com