
���� ��y��ϵ��Ϊa��x��ϵ��Ϊb����$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$���뷽����$\left\{\begin{array}{l}{2x+ay=3}\\{bx+y=3}\end{array}\right.$�ó�$\left\{\begin{array}{l}{4+a=3}\\{2b+1=3}\end{array}\right.$�����������Ľ⣬���ɵó��𰸣�
��� �⣺��y��ϵ��Ϊa��x��ϵ��Ϊb��
��$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$���뷽����$\left\{\begin{array}{l}{2x+ay=3}\\{bx+y=3}\end{array}\right.$�ã�$\left\{\begin{array}{l}{4+a=3}\\{2b+1=3}\end{array}\right.$��
��ã�a=-1��b=1��
����ԭ������Ϊ$\left\{\begin{array}{l}2x-y=3\\ x+y=3\end{array}\right.$��
���� ���⿼���˶�Ԫһ�η�����Ľ⣬���Ԫһ�η������Ӧ�ã��������Ԫһ�η������Ķ����ǽ����Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ȱߡ�ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ�
��ͼ���ȱߡ�ABC������BC����ƽ�Ƶ���DCE��λ�ã�����AD��BD�������н��ۣ�| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ij���尮����ѵ��ʱ��б��ʾ��ͼ�����ڰ�ȫ���ؿ��ǣ�������ѵ����б�µ������45�㽵Ϊ30�㣬��֪ԭб������AB�ij�Ϊ5�ף���D��B��C ��ͬһˮƽ�����ϣ�
��ͼ��ij���尮����ѵ��ʱ��б��ʾ��ͼ�����ڰ�ȫ���ؿ��ǣ�������ѵ����б�µ������45�㽵Ϊ30�㣬��֪ԭб������AB�ij�Ϊ5�ף���D��B��C ��ͬһˮƽ�����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3cm��5cm��8cm | B�� | 1cm��2cm��3cm | C�� | 4cm��5cm��10cm | D�� | 3cm��4cm��5cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
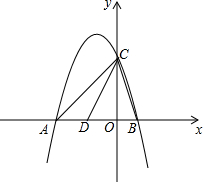 ��ͼ��������y=-x2-2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C��
��ͼ��������y=-x2-2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
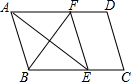 ��ͼ����ƽ���ı���ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F����BF=12��AB=10����AE�ij�Ϊ��������
��ͼ����ƽ���ı���ABCD�У���BAD��ƽ���߽�BC�ڵ�E����ABC��ƽ���߽�AD�ڵ�F����BF=12��AB=10����AE�ij�Ϊ��������| A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 170 | B�� | 400 | C�� | 1�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com