
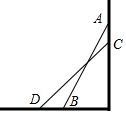
 如图,一根长5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,竹竿底端B外移的距离BD( )
如图,一根长5米的竹竿AB斜靠在一竖直的墙AO上,这时AO为4米,如果竹竿的顶端A沿墙下滑1米,竹竿底端B外移的距离BD( )| A. | 等于1米 | B. | 大于1米 | C. | 小于1米 | D. | 以上都不对 |
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
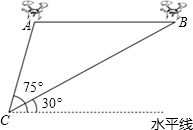 某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)9$\sqrt{3}$+9米.
某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为3米/秒,则这架无人飞机的飞行高度为(结果保留根号)9$\sqrt{3}$+9米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com