
已知抛物线的解析式为
(1)求证:不论m为何值,此抛物线与x轴必有两个交点,且两交点A、B之间的距离为定值;
(2)设点P为此抛物线上一点,若△PAB的面积为8,求符合条件的点P的坐标;
(3)若(2)中△PAB的面积为S(S>0),试根据面积S值的变化情况,确定符合条件的点P的个数(本小题直接写出结论,不要求写出计算、证明过程).
(1)证明见解析;(2)(m,4)或(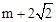 ,−4)或(
,−4)或( ,-4);(3)当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
,-4);(3)当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
【解析】
试题分析:(1)本题需先求出△的值,再证出△>0,再设出A、B的坐标,然后代入公式即可求出AB的长;
(2)本题需先设出P的坐标,再由题意得出b的值,然后即可求出符合条件的所有点P的坐标;
(3)本题需分当s=8时,当0<s<8时,当s>8时三种情况进行讨论,即可得出符合条件的点P的个数.
试题解析::(1)∵△=(2m)2-4×(-1)(4-m2)=16>0,
∴不论m取何值,此抛物线与x轴必有两个交点.
设A(x1,0),B(x2,0),
则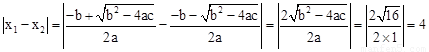 (定值).
(定值).
(2)设P(a,b),则由题意b=-a2+2am+4-m2,且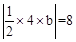 ,
,
解得b=±4.
当b=4时得:a=m,即P(m,4);
当b=-4时得: ,即P(
,即P(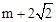 ,−4)或P(
,−4)或P( ,-4).
,-4).
综上所述,符合条件的点P的坐标为(m,4)或(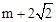 ,−4)或(
,−4)或( ,-4).
,-4).
(3)由(2)知当s=8时,符合条件的点P有3个,当0<s<8时,符合条件的点P有4个,当s>8时,符合条件的点P有2个.
考点:1.二次函数的和性质;2.曲线上点的坐标与方程的关系;3.分类思想的应用.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com