
 ,点P从点B开始沿BC边向终点C以每秒3cm的速度移动,点Q从点D开始沿DA边向终点A以每秒2cm的速度移动,设运动时间为t秒.
,点P从点B开始沿BC边向终点C以每秒3cm的速度移动,点Q从点D开始沿DA边向终点A以每秒2cm的速度移动,设运动时间为t秒.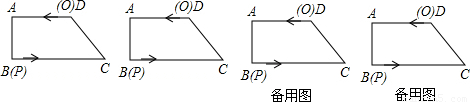
 ,可求得CD,CH的长,又由四边形ABPQ是矩形,可得AQ=BP,即可得方程:12-2t=3t,解此方程即可求得答案;
,可求得CD,CH的长,又由四边形ABPQ是矩形,可得AQ=BP,即可得方程:12-2t=3t,解此方程即可求得答案;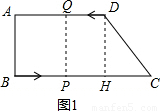 解:(1)如图1,过点D作DH⊥BC,垂足为点H,
解:(1)如图1,过点D作DH⊥BC,垂足为点H,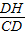 ,
, ,
,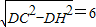 (cm),…(1分)
(cm),…(1分)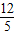 ;…(1分)
;…(1分) 再过点Q作QG⊥BC,垂足为点G,
再过点Q作QG⊥BC,垂足为点G,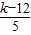 ,…(1分)
,…(1分) ,…(1分)
,…(1分)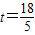 ,…(1分)
,…(1分)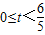 和
和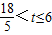 时,⊙P与⊙Q外离;…(2分)
时,⊙P与⊙Q外离;…(2分)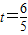 和
和 时,⊙P与⊙Q外切;
时,⊙P与⊙Q外切; 时,⊙P与⊙Q相交.…(2分)
时,⊙P与⊙Q相交.…(2分)

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.
如图,在梯形ABCD中,AB∥CD,E是AB边上的点,给出下面三个论断:①AD=BC;②DE=CE;③AE=BE.请你以其中的两个论断为条件,填入“已知”栏中,以一个论断作为结论,填入“求证”栏中,使之成为一个正确的命题,并证明之.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.
如图,在梯形ABCD中,AD∥BC,AD=AB,过点A作AE∥DB交CB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
| 8 |
| 5 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com