
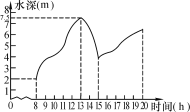
【题目】如图所示是某港口从上午8 h到下午8 h的水深情况,根据图象回答下列问题:
(1)在8 h到20 h,这段时间内大约什么时间港口的水位最深,深度是多少米?
(2)大约什么时候港口的水位最浅,是多少?
(3)在这段时间里,水深是如何变化的?
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形. 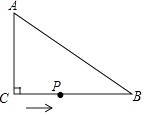
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天小明和同学们去郊外爬山,得到如下数据:
爬坡长度x(m) | 40 | 80 | 120 | 160 | 200 | 240 |
爬坡时间t(min) | 2 | 5 | 9 | 14 | 20 | 30 |
(1)当爬到120 m时,所用时间是多少?
(2)爬坡速度随时间是怎样变化的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,淇淇的爸爸去参加一个聚会,淇淇坐在汽车上用所学知识绘制了一张反映汽车速度与时间的关系图,第二天,淇淇拿着这张图给同学看,并向同学提出如下问题,你能回答吗?
(1)在上述变化过程中,自变量是什么?因变量是什么?
(2)汽车从出发到最后停止共经过了多长时间?它的最高时速是多少?
(3)汽车在哪段时间保持匀速行驶?速度是多少?
(4)用语言大致描述这辆汽车的行驶情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是 . 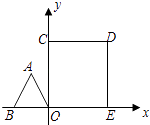
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=BC=5,AB=5![]() ,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.
,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙用4张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上,每人抽一张,甲先抽,乙后抽,抽出的牌不放回.甲、乙约定:只有甲抽到的牌面数字比乙大时甲胜;否则乙胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.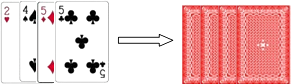
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com