
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
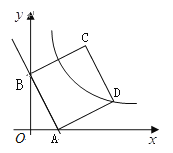
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
【答案】(1)A![]() ,B
,B![]() ;(2)①证明见解析②点C恰好落在双曲线
;(2)①证明见解析②点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
【解析】试题分析:(1)分别令x=0,求出y的值;令y=0,求出x的值即可得出点B与点A的坐标;
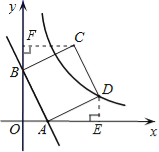
(2)①过点D作DE⊥x轴于点E,由全等三角形的性质可得出△AOB≌△DEA,故可得出AB=AD,再利用待定系数法求出直线AD的解析式即可得出AB⊥AD,由此可得出结论;
②过点C作CF⊥y轴,利用△AOB≌△DEA,同理可得出:△AOB≌△BFC,即可得出C点纵坐标,如果点在图象上,利用纵坐标求出横坐标即可.
解:(1)∵令x=0,则y=2;令y=0,则x=1,
∴A(1,0),B(0,2).
故答案为:(1,0),(0,2);
(2)①过点D作DE⊥x轴于点E,
∵A(1,0),B(0,2),D(3,1),
∴AE=OB=2,OA=DE=1,
在△AOB与△DEA中,
![]() ,
,
∴△AOB≌△DEA(SAS),
∴AB=AD,
设直线AD的解析式为y=kx+b(k≠0),
∴![]() ,
,
解得![]() ,
,
∵(﹣2)×=﹣1,
∴AB⊥AD,
∵四边形ABCD是正方形;
②过点C作CF⊥y轴,
∵△AOB≌△DEA,
∴同理可得出:△AOB≌△BFC,
∴OB=CF=2
∵C点纵坐标为:3,
代入y=,
∴x=1,
∴应该将正方形ABCD沿X轴向左平移2﹣1=1个单位长度时,点C的对应点恰好落在(1)中的双曲线上.


科目:初中数学 来源: 题型:
【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
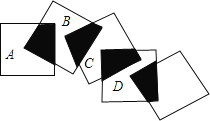
A.2cm2 B.4cm2 C.6cm2 D.8cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.
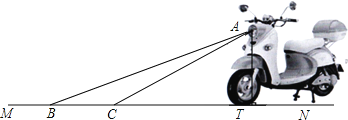
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠C=![]() ,∠EAC+∠FBC=
,∠EAC+∠FBC=![]()
(1)如图①,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则![]() 与
与![]() 有何关系?并说明理由.
有何关系?并说明理由.

(2)如图②,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与![]() 、
、![]() 的关系是 .(用
的关系是 .(用![]() 、
、![]() 表示)
表示)

(3)如图③,若![]() ≥
≥![]() ,∠EAC与∠FBC的平分线相交于
,∠EAC与∠FBC的平分线相交于![]() ,
, ![]() ;依此类推,则
;依此类推,则![]() = (用
= (用![]() 、
、![]() 表示)
表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城总长约为6 700 000米,用科学记数法表示正确的是( )
A. 6.7×108米 B. 6.7×107米 C. 6.7×106米 D. 6.7×105米
查看答案和解析>>
科目:初中数学 来源: 题型:
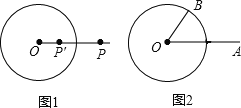
【题目】如图1,⊙O的半径为r(r>0),若点P′在射线OP上,满足OP′OP=r2,则称点P′是点P关于⊙O的“反演点”.
如图2,⊙O的半径为4,点B在⊙O上,∠BOA=60°,OA=8,若点A′,B′分别是点A,B关于⊙O的反演点,求A′B′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
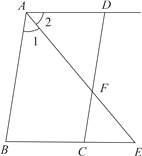
∵AB∥DC(已知)
∴∠1=∠CFE( )
∵AE平分∠BAD(已知)
∴∠1= ∠2 (角平分线的定义)
∵∠CFE=∠E(已知)∴∠2= (等量代换)
∴AD∥BC( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在△ABC中,∠A=40°.
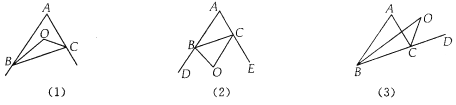
(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;
(2)如图(2)若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
(3)如图(3)若BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;
(4)根据上述三问的结果,当∠A=n°时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com