
 如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.
如图,在平面直角坐标系xOy中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,2),B(n,-1),其中m>0,n<0.分析 (1)利用反比例函数图象上点的坐标特征可求出m与n之间的数量关系;
(2)根据题意和勾股定理即可得到关于m的方程,解方程求得A、B的坐标,然后根据待定系数法求得即可.
解答 解:(1)∵点A(m,2),B(n,-1)在双曲线y=$\frac{k}{x}$上,
∴k=2m=-n,
即n=-2m;
(2)∵OA=OB,点A(m,2),B(-2m,-1),
∴OA2=OB2,即m2+22=(-2m)2+(-1)2,
解得m1=1,m2=-1(舍去),
∴A(1,2),B(-2,-1),
∴k=1×2=2,
∴所求双曲线的解析式为y=$\frac{2}{x}$,
设所求的直线的解析式为y=kx+b,
把A、B的坐标代入得$\left\{\begin{array}{l}{2=k+b}\\{-1=-2k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴所求的直线的解析式为y=x+1.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数和反比例函数的解析式解题的关键是利用勾股定理求得A、B的坐标.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:填空题
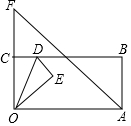 如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
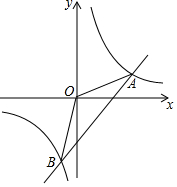 如图,在平面直角坐标系中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,3),B(-2,n),其中m>0,n<0
如图,在平面直角坐标系中,不经过原点的直线与双曲线y=$\frac{k}{x}$相交于点A(m,3),B(-2,n),其中m>0,n<0查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+6与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{2}$x交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 汽车沿一条公路从A地驶往B地所需的时间t与平均速度v | |
| B. | 圆的周长l与圆的半径r | |
| C. | 圆的面积s与圆的半径r | |
| D. | 在电阻不变的情况下,电流强度I与电压U |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{2}b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com