解:(1)设直线m的解析式为:y=kx+b,
∵直线过(-4,1),(2,4)两点,
∴
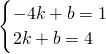
,
解得:
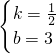
,
∴直线m的解析式为:y=

x+3;
(2)
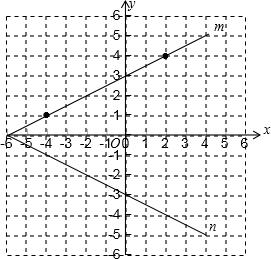
∵直线n与直线m关于x轴对称,
∴-y=

x+3,
∴直线n的解析式为:y=-

x-3.
分析:(1)首先设出一次函数解析式,然后利用待定系数法,把(-4,1),(2,4)两点坐标代入解析式即可得到k,b的值,进而可以得到解析式;
(2)根据直线y=kx+b,(k≠0,且k,b为常数)关于x轴对称的规律:就是x不变,y变成-y:-y=kx+b,即y=-kx-b,求出解析式后,再画出图象.
点评:此题主要考查了待定系数法求一次函数解析式,以及一次函数图象与几何变换,关键是熟记变换规律:直线y=kx+b,(k≠0,且k,b为常数)
①关于x轴对称,就是x不变,y变成-y:-y=kx+b,即y=-kx-b;
(关于X轴对称,横坐标不变,纵坐标是原来的相反数)
②关于y轴对称,就是y不变,x变成-x:y=k(-x)+b,即y=-kx+b;
(关于y轴对称,纵坐标不变,横坐标是原来的相反数)
③关于原点对称,就是x和y都变成相反数:-y=k(-x)+b,即y=kx-b.
(关于原点轴对称,横、纵坐标都变为原来的相反数)

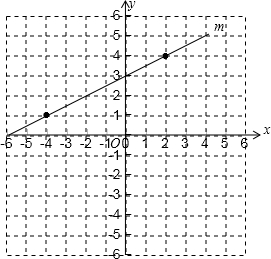 已知直线m经过(-4,1),(2,4)两点.
已知直线m经过(-4,1),(2,4)两点.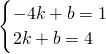 ,
,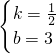 ,
, x+3;
x+3;
 x+3,
x+3, x-3.
x-3.
