已知关于x函数y=(2-k)x2-2x+k
(1)若此函数的图象与坐标轴只有2个交点,求k的值.
(2)求证:关于x的一元二次方程(2-k)x2-2x+k=0必有一个根是1.
(1)解:分情况讨论:
(i)k-2=0时,得k=2.
此时y=-2x+2与坐标轴有两个交点,符合题意;
(ⅱ)k-2≠0时,得到一个二次函数,
①抛物线与x轴只有一个交点,△=b
2-4ac=(-2)
2-4k(2-k)=4(k-1)
2,
解得k=1;
②抛物线与x轴有两个交点,其中一个交点是(0,0),
把(0,0)代入函数解析式,易得k=0;
故答案为:2或0或1.
(2)证明:设关于x的一元二次方程(2-k)x
2-2x+k=0的两个实数根分别为x
1,x
2,
∴

,
∴
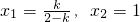
,
∴关于x的一元二次方程(2-k)x
2-2x+k=0必有一个根是1.
分析:(1)分情况讨论:(i)k-2=0时,求出k.(ⅱ)k-2≠0时,得到一个二次函数,①抛物线与x轴只有一个交点,△=4(k-1)
2,求出k;②抛物线与x轴有两个交点,其中一个交点是(0,0),把(0,0)代入函数解析式,求出k.
(2)设关于x的一元二次方程(2-k)x
2-2x+k=0的两个实数根分别为x
1,x
2,根据公式求出方程的解即可得到答案.
点评:本题主要考查对抛物线与x轴的交点,一次函数的性质,根的判别式,根与系数的关系,解一元二次方程-公式法等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

 ,
,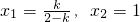 ,
,

 阅读快车系列答案
阅读快车系列答案